Тригонометричні рівняння
У тригонометричних рівняннях невідоме з’являється в аргументі тригонометричних функцій, наприклад, \sin x = 2 \cos (x+\pi). Якщо не зазначено інше, припускаємо, що аргументи тригонометричних функцій у радіанах.
Запис виразів з тригонометричними функціями та пріоритет операцій
У запису виразів з тригонометричними функціями часто опускаємо дужки навколо аргументу (пишемо \sin x замість \sin(x)), якщо зрозуміло, що є аргументом тригонометричної функції.
Важливо при читанні виразів із тригонометричними функціями розуміти, яка операція буде виконана раніше. Наприклад, \cos x + 2 не є тим самим, що \cos(x+2), тому що функцію \cos застосовуємо у виразі без дужок раніше, ніж додавання або віднімання. Зазвичай \sin 2x розуміємо як \sin (2x), але коли маємо вираз \sin x \sin x, розуміємо його як \sin (x) \cdot \sin (x).
Степені значень тригонометричних функцій також мають свій спеціальний запис:
| \sin^2 x | квадрат виразу \sin x |
| \sin x + 1 | сума \sin(x) a 1 |
| \sin (x+1) | синус суми x+1 |
| \sin 3y | синус добутку 3\cdot y |
| \sin x \tan y | добуток \sin (x) a \tan (y) |
Поради для розв’язання тригонометричних рівнянь
Крім знань про значення, властивості та графіки тригонометричних функцій, можуть знадобитися також:
- тригонометричні формули,
- так звана тригонометрична одиниця – співвідношення \sin^2 x + \cos^2 x = 1, яке діє для будь-якого дійсного x,
- підстановка, наприклад, \cos^2 x -2 \cos x +1 = 0 можна спочатку розв’язати як квадратне рівняння t^2 -2t +1 pro t=\cos x, а вже для знайдених значень t шукати відповідні значення x.
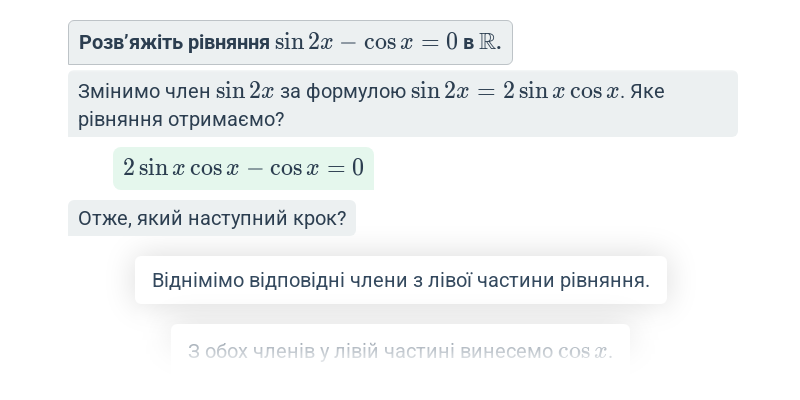
Крок за кроком
Доповнення окремих кроків в рамках комплексної роботи.