Дякуємо за Ваш відгук.

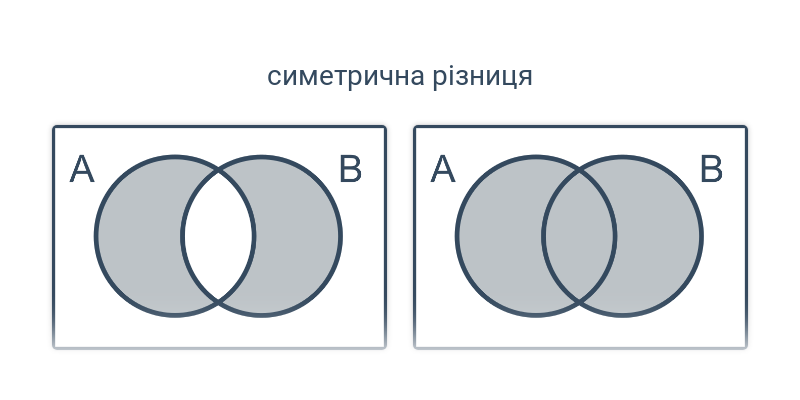
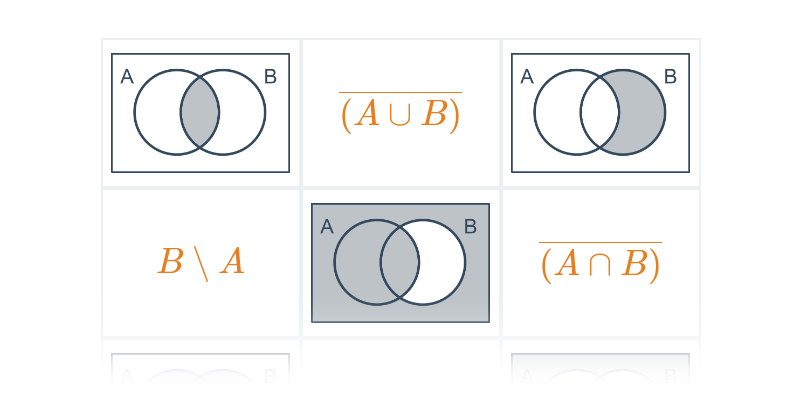
Множини: основні поняття

Множина — це набір елементів. У множині не важливий порядок елементів і не враховуються повторювані елементи. Такі множини є однаковими:

Позначення	Поняття	Коментар
\emptyset	порожня множина
\overline{A}	доповнення	елементи, які не належать до множини A
x \in A	належить множині	елементи x належать до множини A
A \cap B	перетин	елементи, які належать до обох множин A, B
A \cup B	об’єднання	елементи, які належать принаймні до однієї з множин A, B
A \setminus B	різниця	елементи, які належать до множини A, але не належать до B
A = B	рівність	рівність множин A, B
A \subseteq B	підмножина	усі елементи множини A належать і до множини B
A \subset B	власна підмножина	A є підмножиною B і одночасно A \neq B
\|A\|	розмір множини	кількість елементів множини
A \cap B = \emptyset	диз’юнктні множини	множини A, B не мають жодного спільного елемента