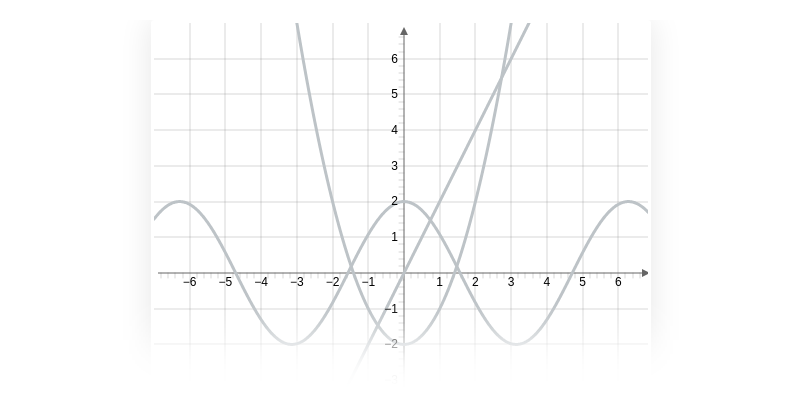
Властивості функцій – 3 клас

Примітка: для спрощення опису розглядаємо лише функції, область визначення яких складається з усіх дійсних чисел.

Функція f називається парною, якщо для кожного x виконується f(-x) = f(x). Графік парної функції є симетричним відносно осі y. Приклади парних функцій: f_1(x) = x^2, f_2(x) = \cos(x), f_3(x) = x^4-3x^2+2.

Функція f називається непарною, якщо для кожного x виконується f(-x) = -f(x). Графік непарної функції є симетричним відносно початку координат. Приклади непарних функцій: f_1(x) = 3x, f_2(x) = \sin(x), f_3(x) = x^3-2x.

Функція f називається періодичною, якщо існує число p != 0 (період функції) таке, що для кожного x виконується f(x+p)=f(x). Типовими прикладами періодичних функцій є тригонометричні функції. Натомість, наприклад, многочлени не є періодичними (за винятком постійної функції).

Функція f називається обмеженою знизу, якщо існує таке число k, що для кожного x виконується f(x) \geq k. Функція f називається обмеженою зверху, якщо існує таке число k, що для кожного x виконується f(x) \leq k. Функція f називається обмеженою, якщо вона одночасно обмежена зверху і знизу. Приклади:

• Функція f(x) = \sin(x) є обмеженою.
• Функція f(x) = x^2 є обмеженою знизу (оскільки \forall x: f(x) \geq 0), але не є обмеженою зверху.
• Функція f(x) = 2x не є обмеженою ні зверху, ні знизу.

Функція f називається простою, якщо для кожної пари x_1 \neq x_2 виконується f(x_1) \neq f(x_2).

Функція f називається зростаючою, якщо для кожної пари x_1 < x_2 виконується f(x_1) < f(x_2).

Функція f називається спадною, якщо для кожної пари x_1 > x_2 виконується f(x_1) > f(x_2).