Дякуємо за Ваш відгук.

Тригонометричні функції та прямокутний трикутник

Тригонометричні функції можна виразити у прямокутному трикутнику таким чином:

Синус (\sin) кута \alpha − це відношення довжини протилежного катета до довжини гіпотенузи.
Косинус (\cos) кута \alpha − це відношення довжини прилеглого катета до довжини гіпотенузи.
Тангенс (\tan) кута \alpha − це відношення довжини протилежного катета до довжини прилеглого катета.

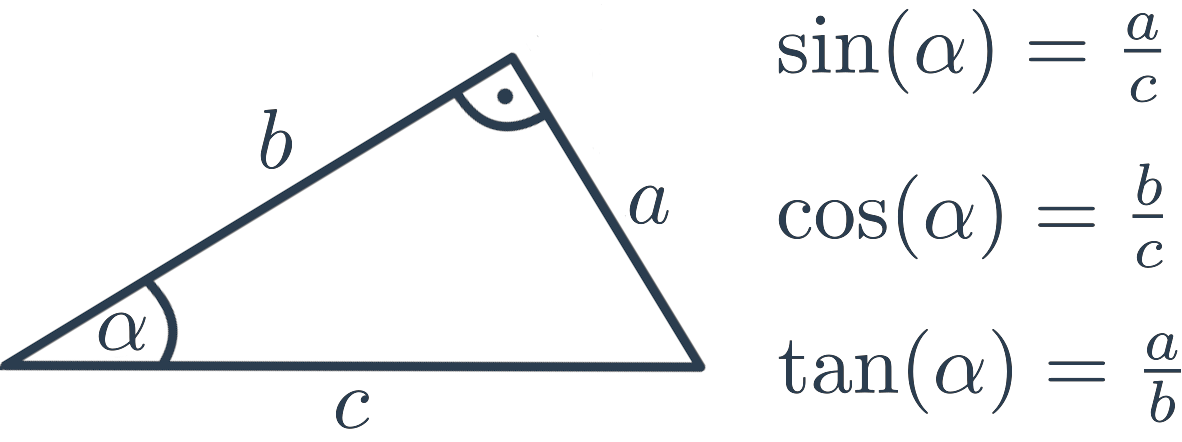
Якщо пам’ятати визначні значення тригонометричних функцій (наприклад, \sin 30^{\circ}=\frac{1}{2}) або хоча б мати доступ до калькулятора чи математичних таблиць, тобто знати значення \sin, \cos або \tan якого-небудь кута у прямокутному трикутнику, то це означає знати розмір самого кута.

Приклад: знаємо сторони прямокутного трикутника, обчислюємо кути

Прямокутний трикутник ABC має довжини сторін a=24, b=10, c=26. Які розміри його внутрішніх кутів?

Якщо трикутник прямокутний, то розмір кута \gamma навпроти найдовшої сторони c дорівнює 90^{\circ}.
Ми знаємо, що \sin \alpha − це відношення протилежної сторони до гіпотенузи, тобто \sin \alpha=\frac{a}{c}.
Підставимо відомі довжини сторін: \sin \alpha = \frac{24}{26}\doteq 0{,}923
Відповідно, розмір кута це: \alpha \doteq 67^{\circ}
Z \alpha+\beta+\gamma=180^{\circ} обчислюємо, що \beta приблизно дорівнює 23^{\circ}.

Перевірка:

Ми знаємо, що \cos \beta − це відношення прилеглої до кута \beta сторони до гіпотенузи, тобто \cos \beta = \frac{a}{c}.
Підставимо відомі довжини сторін: \cos \beta = \frac{24}{26}\doteq 0{,}923
Відповідний розмір кута: \beta \doteq 23^{\circ}

Приклад: знаємо кут, обчислюємо довжину сторони за допомогою \sin

Нехай маємо прямокутний трикутник ABC з прямим кутом у вершині C, в якому \sin \alpha = \frac{1}{2} і довжина гіпотенузи c=10. Яка довжина сторони a?

Ми знаємо, що значення \sin \alpha обчислюється, як відношення довжини сторони, протилежної куту \alpha, до довжини гіпотенузи, тобто \sin \alpha = \frac{a}{c}.
Підставимо в цю рівність за \sin \alpha і за c.
\frac{1}{2} = \frac{a}{10} \Rightarrow a=5
Довжина сторони a дорівнює 5.

Приклад: знаємо кут, обчислюємо довжину сторони за допомогою \cos

Нехай маємо прямокутний трикутник ABC з прямим кутом у вершині C, в якому \cos \alpha = \frac{3}{5} і довжина гіпотенузи c=15. Яка довжина сторони a?

Ми знаємо, що значення \cos \alpha обчислюється, як відношення довжини сторони, прилеглої до кута \alpha, до довжини гіпотенузи, тобто \cos \alpha = \frac{b}{c}.
Підставимо в цю рівність за \cos \alpha і за c.
\frac{3}{5} = \frac{b}{15} \Rightarrow b=9
Довжина сторони b дорівнює 9. Ми хотіли обчислити довжину сторони a, що можна зробити з відомих значень b,c за допомогою теореми Піфагора.
a^2 = c^2-b^2=255-81=144 \Rightarrow a=12
Довжина сторони a дорівнює 12.

Приклад: знаємо кут, обчислюємо довжину сторони за допомогою \tan

Нехай маємо прямокутний трикутник ABC з кутом \alpha = 60^{\circ} і довжиною більшого катета 6. Яка довжина іншого катета?

Ми знаємо, що у прямокутному трикутнику ABC внутрішні кути 60^{\circ}, 90^{\circ}, обчислюємо відсутній кут.
\beta=180^{\circ}-60^{\circ}-90^{\circ}=30^{\circ}
Ми бачимо, що \beta < \alpha.
Більший катет буде у трикутнику навпроти більшого кута, отже, a=6.
\tan \alpha − це відношення катета, протилежного куту \alpha до прилеглого катета, тобто \tan \alpha = \frac{a}{b}.
Підставимо значення \tan \alpha, значення \tan 60^{\circ} = \sqrt{3} (знаходимо в таблицях або за допомогою калькулятора), підставимо також b=6.
\sqrt{3} = \frac{6}{b} \Rightarrow b= \frac{6}{\sqrt{3}} = 2\sqrt{3}
Отже, довжина меншого катета b=2\sqrt{3}.