Теорема Піфагора: основи
Теорема Піфагора дозволяє обчислити довжину третьої сторони прямокутного трикутника, якщо відомі довжини двох інших сторін:
Довжина гіпотенузи c = \sqrt{a^2 + b^2}. Якщо у прямокутному трикутнику довжини катетів 3 метри і 6 метрів, то гіпотенуза має довжину \sqrt{3^2+6^2} = \sqrt{9+36} = \sqrt{45} \doteq 6{,}41 метра.
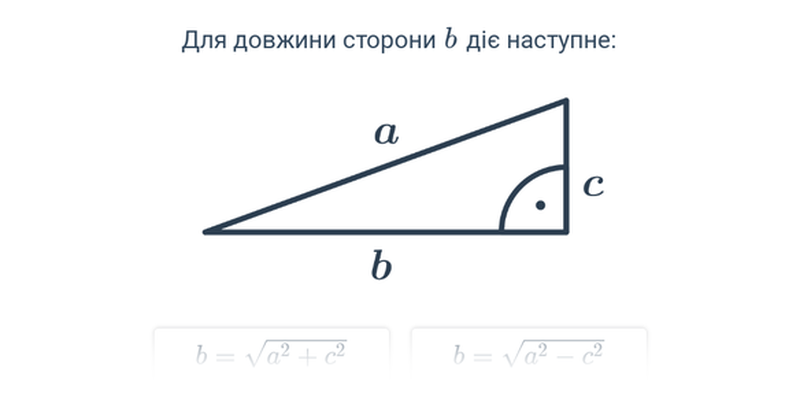
Довжина катета a = \sqrt{c^2-b^2}. Якщо гіпотенуза трикутника має довжину 8 метрів, а один з катетів має довжину 4 метри, то другий катет має довжину \sqrt{8^2-4^2} = \sqrt{64-16} = \sqrt{48} \doteq 6{,}93 метра.
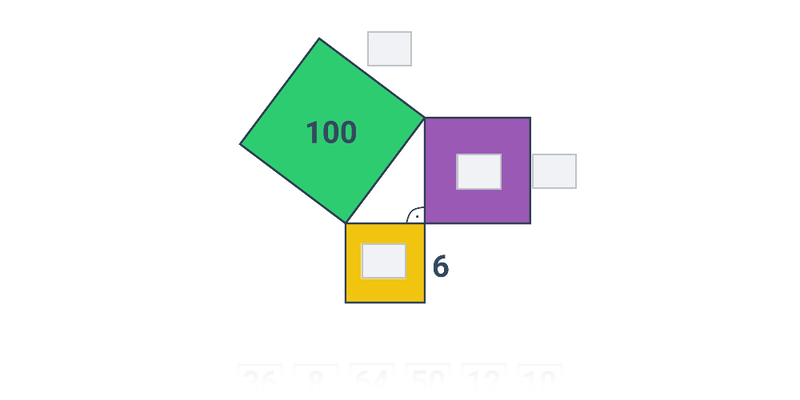
Піфагорові трійки – це три натуральних і цілих числа, які задовольняють рівність a^2+b^2=c^2, тобто трикутник з відповідними довжинами сторін є прямокутним. Типовим прикладом піфагорової трійки є (3, 4, 5): 3^2 + 4^2 = 9+16 = 25 = 5^2.
Інші приклади Піфагорових трійок: (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (9, 40, 41). До Піфагорових трійок належать також усі кратні їм трійки, наприклад: (6, 8, 10); (9, 12, 15); (10, 24, 26). Якщо ми запам’ятаємо деякі основні Піфагорові трійки, особливо найпростішу трійку (3, 4, 5), це може дуже полегшити обчислення.
Переміщення
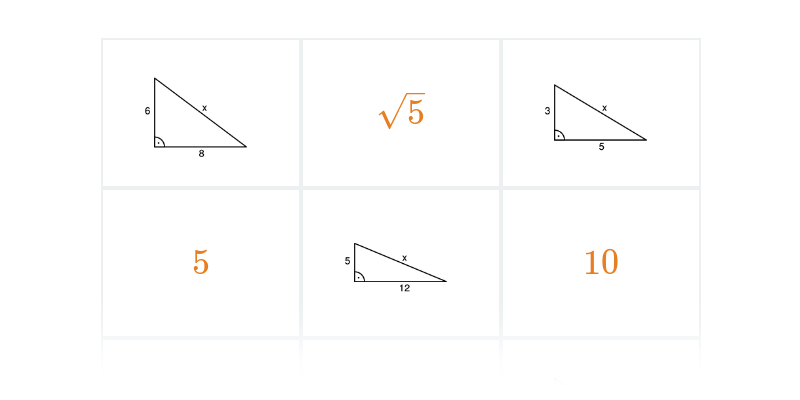
Переміщення карт на правильне місце. Просте управління, цікаві та оригінальні завдання.
Вибір
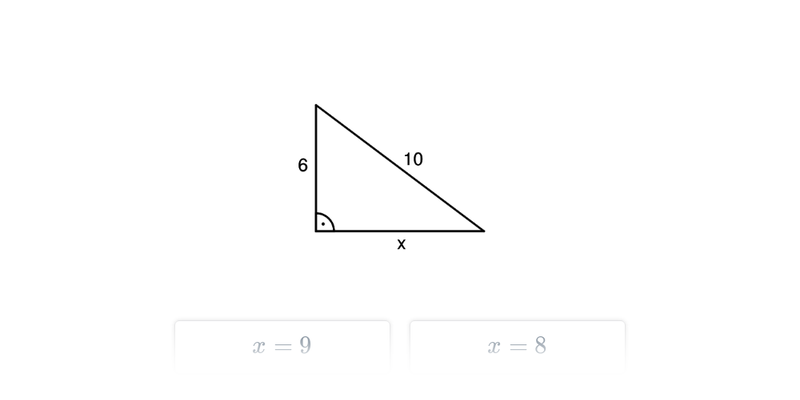
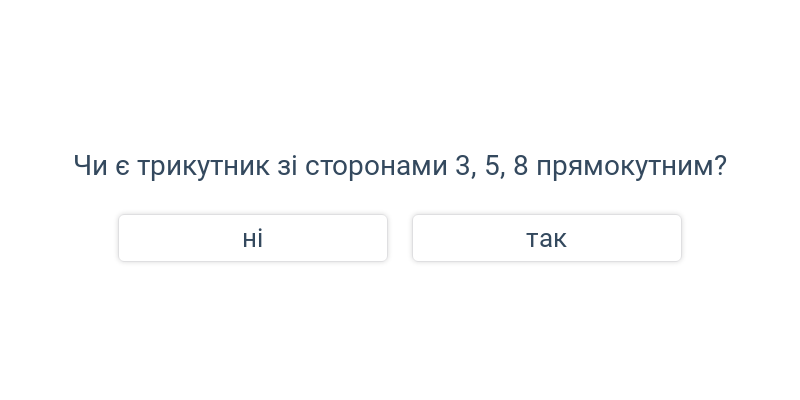
Швидке практикування шляхом вибору з двох варіантів.
Письмова відповідь
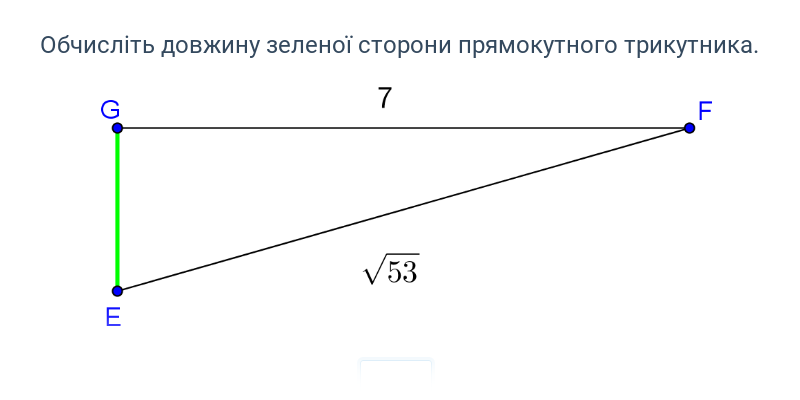
Вправа, в якій ви набираєте відповідь на клавіатурі.