Дякуємо за Ваш відгук.

Площа сектора круга

Площу сектора з центральним кутом $\alpha$ і радіусом $r$ обчислюємо за формулою: $\frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2$

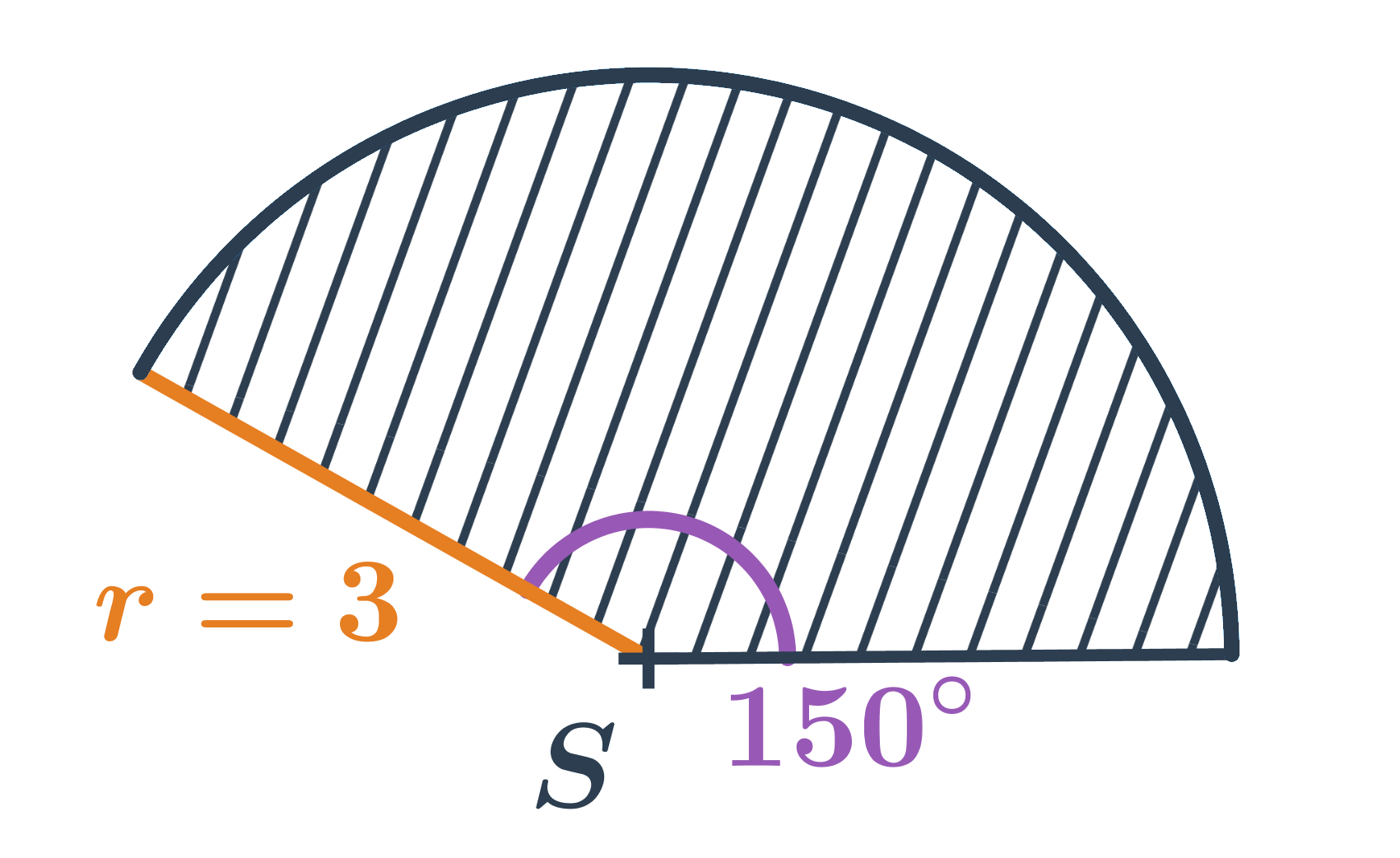
Сектор на малюнку має площу: $\frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi$

Площа цілого кола (сектора з центральним кутом $360^{\circ}$ ) дорівнює: $\frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2$

Вибір

Швидке практикування шляхом вибору з двох варіантів.

Площа сектора круга

Вибір • середній

Вправа, в якій ви набираєте відповідь на клавіатурі.

Площа сектора круга

Письмова відповідь • середній