Піднесення до степеня
Степінь – це добуток однакових множників. Приклади:
- 3^2 = 3\cdot 3 = 9
- 2^3 = 2\cdot 2 \cdot 2= 8
- 5^4 = 5\cdot 5\cdot 5\cdot 5 = 625
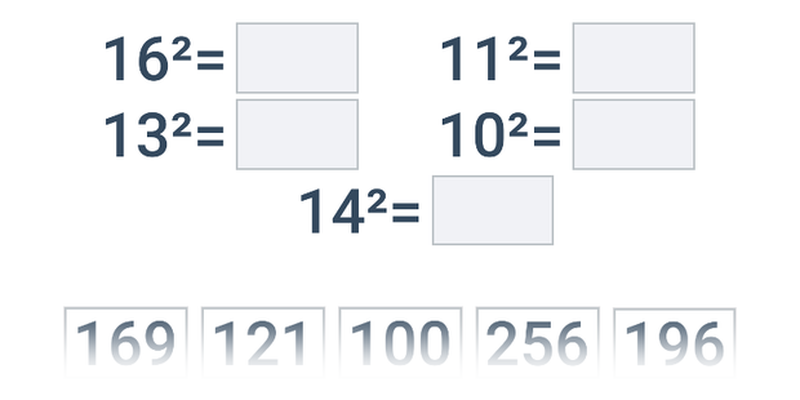
Таблиця квадратів чисел від 1 до 20
| 1^2 | = | 1 |
| 2^2 | = | 4 |
| 3^2 | = | 9 |
| 4^2 | = | 16 |
| 5^2 | = | 25 |
| 6^2 | = | 36 |
| 7^2 | = | 49 |
| 8^2 | = | 64 |
| 9^2 | = | 81 |
| 10^2 | = | 100 |
| 11^2 | = | 121 |
| 12^2 | = | 144 |
| 13^2 | = | 169 |
| 14^2 | = | 196 |
| 15^2 | = | 225 |
| 16^2 | = | 256 |
| 17^2 | = | 289 |
| 18^2 | = | 324 |
| 19^2 | = | 361 |
| 20^2 | = | 400 |
Під час піднесення до степеня від’ємних чисел результат є додатним для парних степенів і від’ємним для непарних.
- (-3)^2 = (-3)\cdot (-3) = 9
- (-3)^3 = (-3)\cdot (-3)\cdot (-3) = -27
- (-3)^4 = (-3)\cdot (-3)\cdot (-3)\cdot (-3) = 81
Нульовий степінь будь-якого числа дорівнює 1 (наприклад, 5^0=1, 564^0=1). Нуль, піднесений до будь-якого степеня, дорівнює 0 (наприклад, 0^3 = 0\cdot 0\cdot 0 = 0). Це веде до цікавого питання: чому дорівнює 0^0?
Переміщення
Переміщення карт на правильне місце. Просте управління, цікаві та оригінальні завдання.
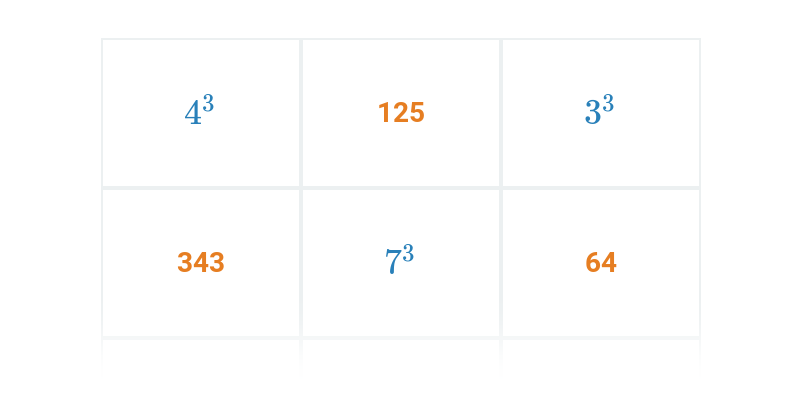
Вибір
Швидке практикування шляхом вибору з двох варіантів.
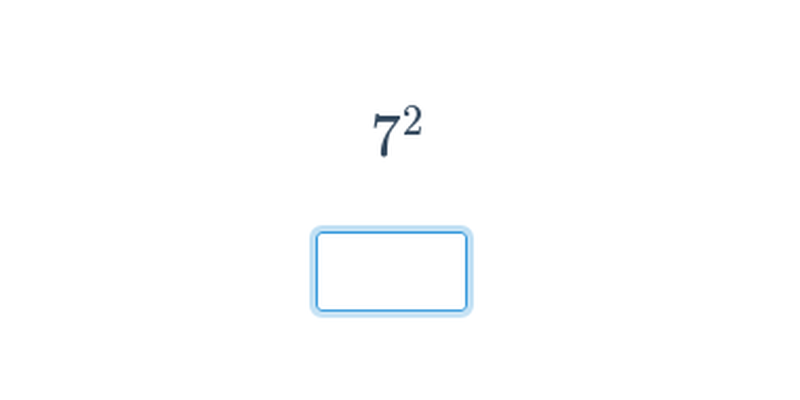
Письмова відповідь
Вправа, в якій ви набираєте відповідь на клавіатурі.