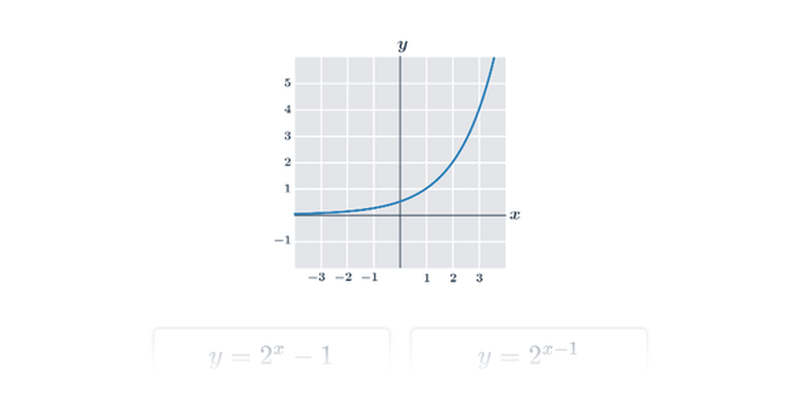
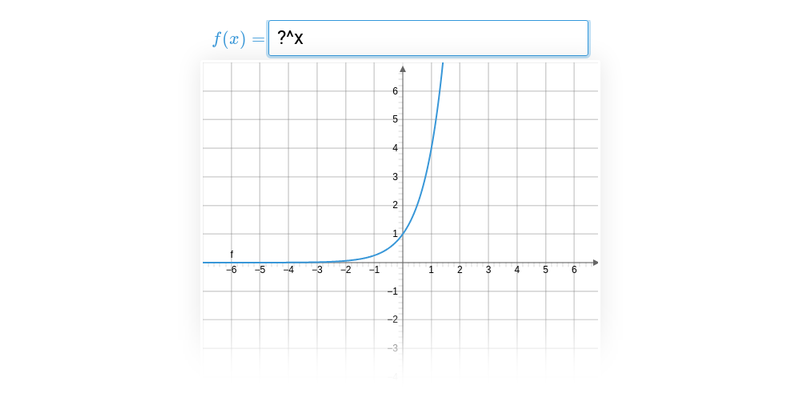
Графіки показникової та логарифмічної функцій
Графіки експоненційних функцій
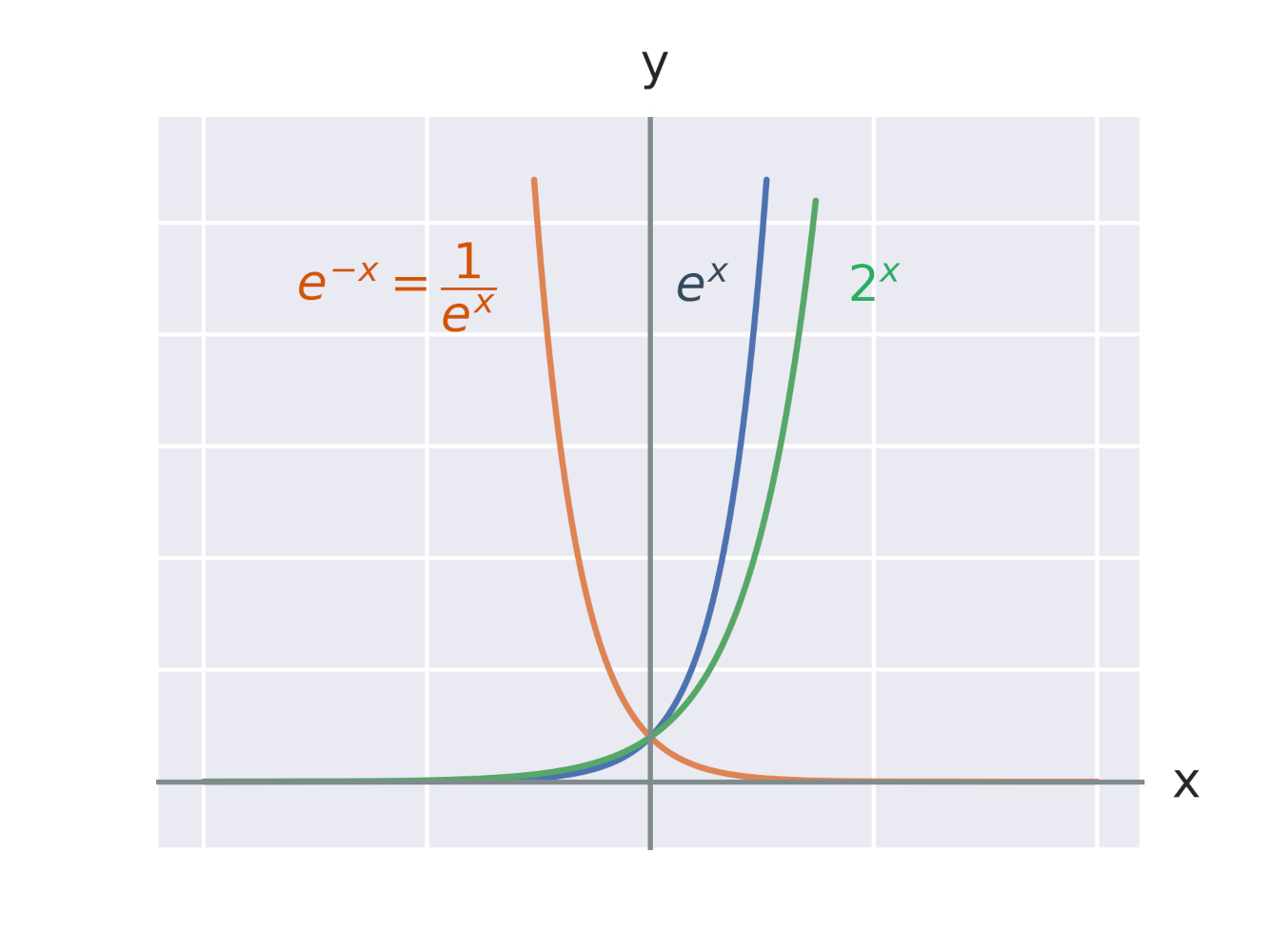
Графіком експоненційної функції є крива під назвою експонента. На рисунку показано графіки експоненційних функцій з основами 2 і e = 2{,}7 182 818 284\ldots Ми також бачимо, що графіки функцій e^x та e^{-x} є симетричними відносно осі y.
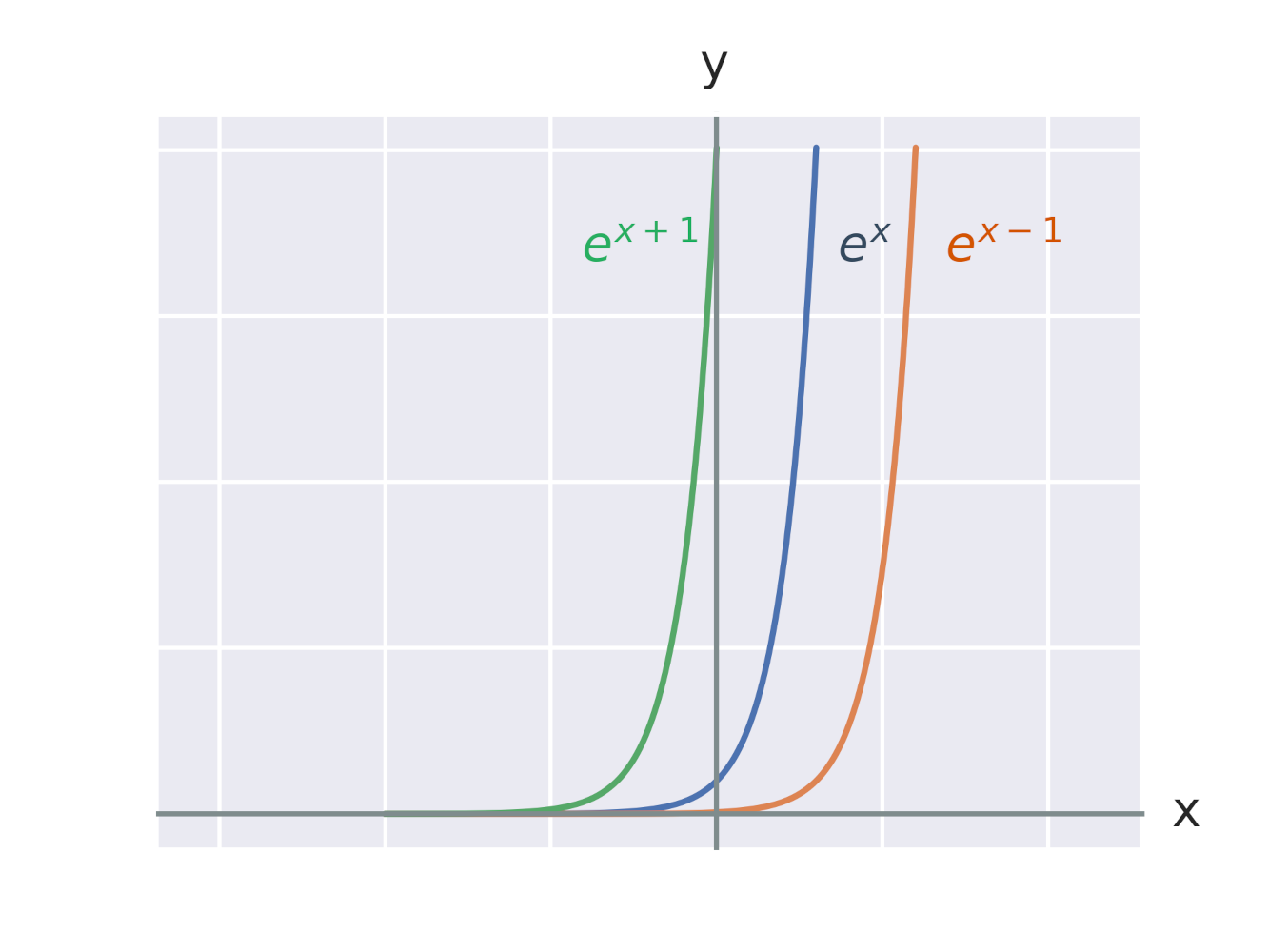
Ефект додавання константи до експоненційної функції
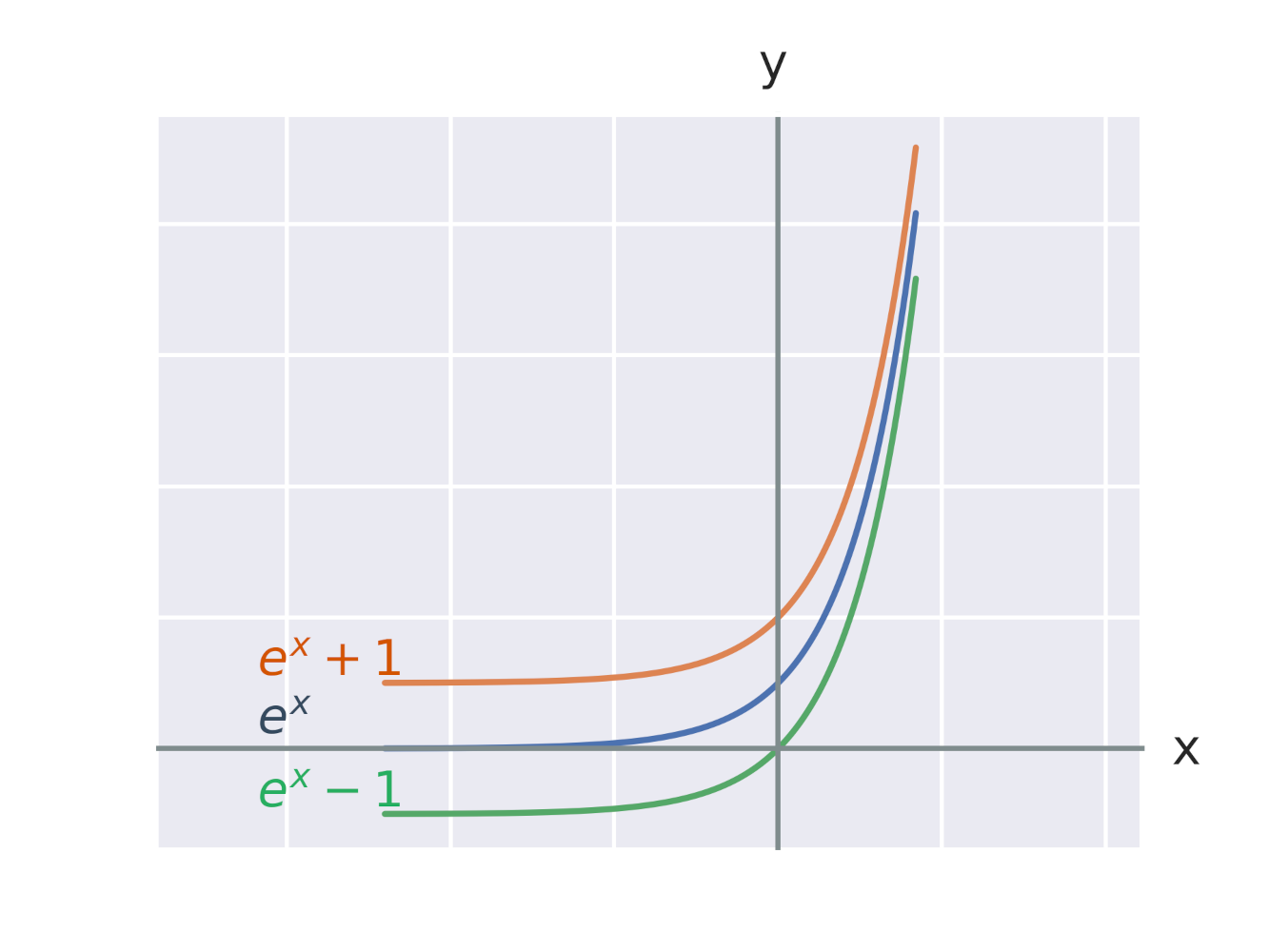
Ефект додавання константи до експонента
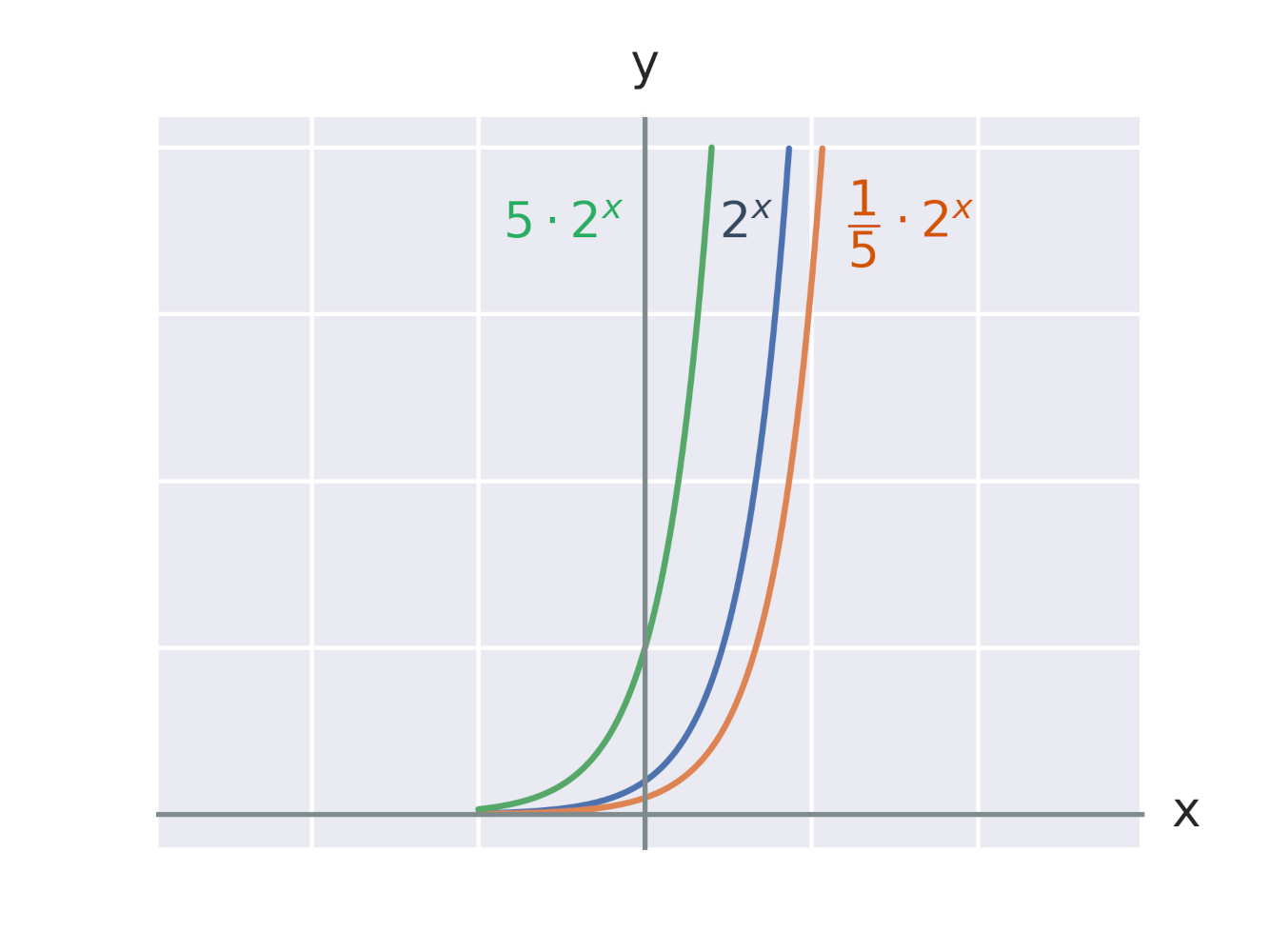
Ефект множення експоненційної функції на константу
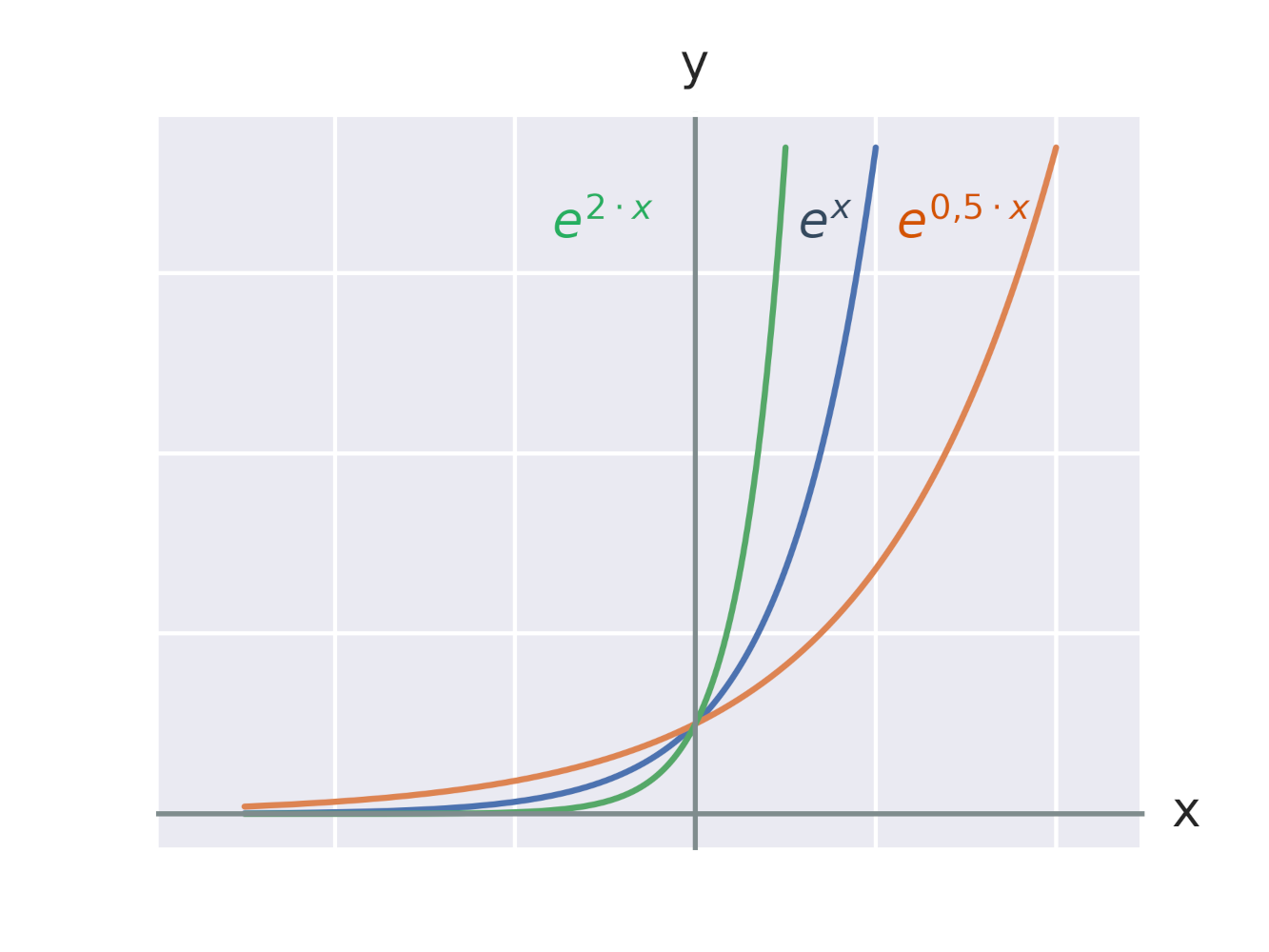
Ефект множення експонента на константу
Графіки логарифмічних функцій
Логарифмічна функція є оберненою до експоненційної функції з тією самою основою. Графіки двох взаємно обернених функцій є симетричними відносно осі першого квадранта (прямої, що відповідає x=y).
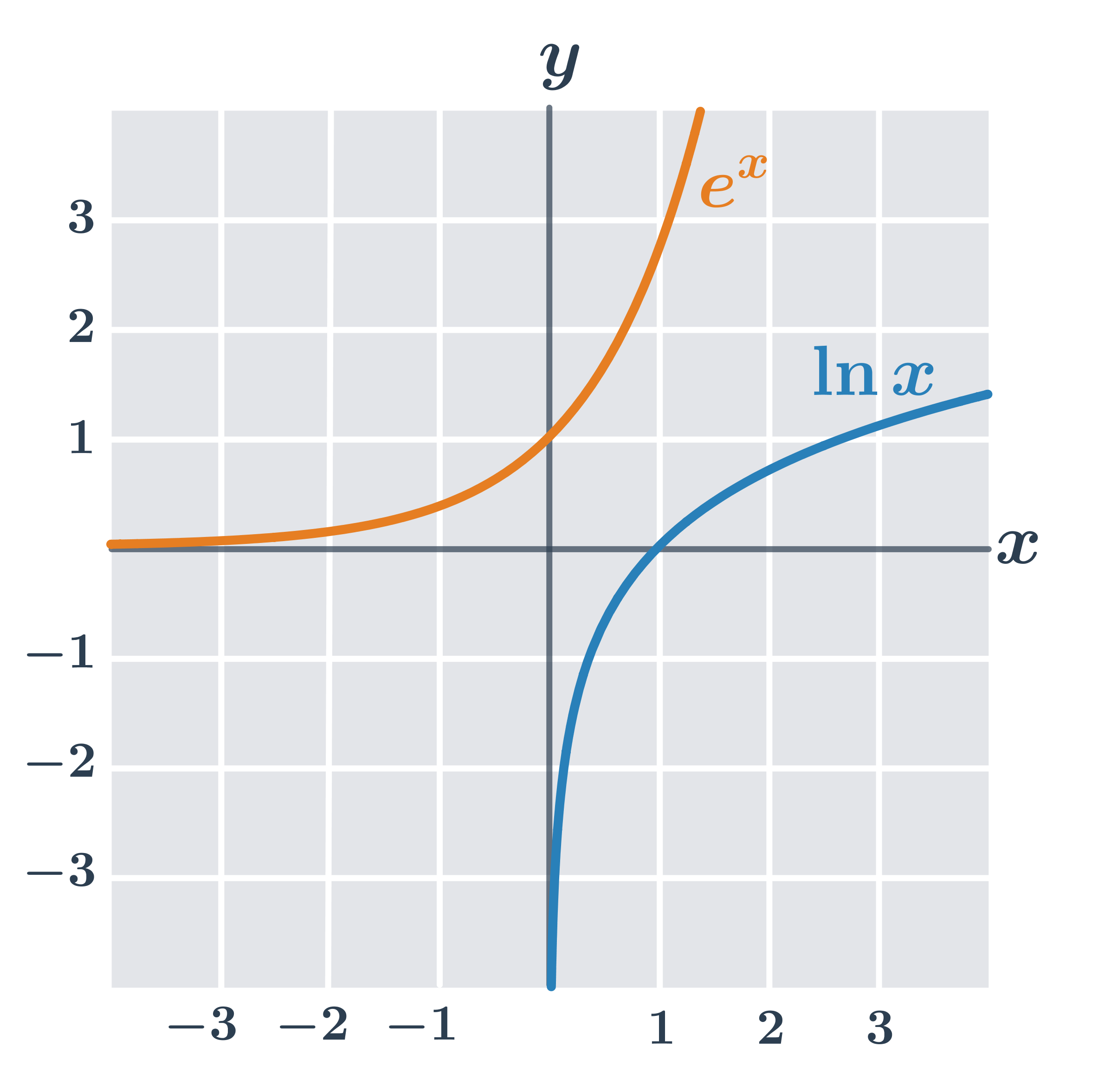
На рисунку показано графіки логарифмічних функцій з різними основами 2, e, 10.
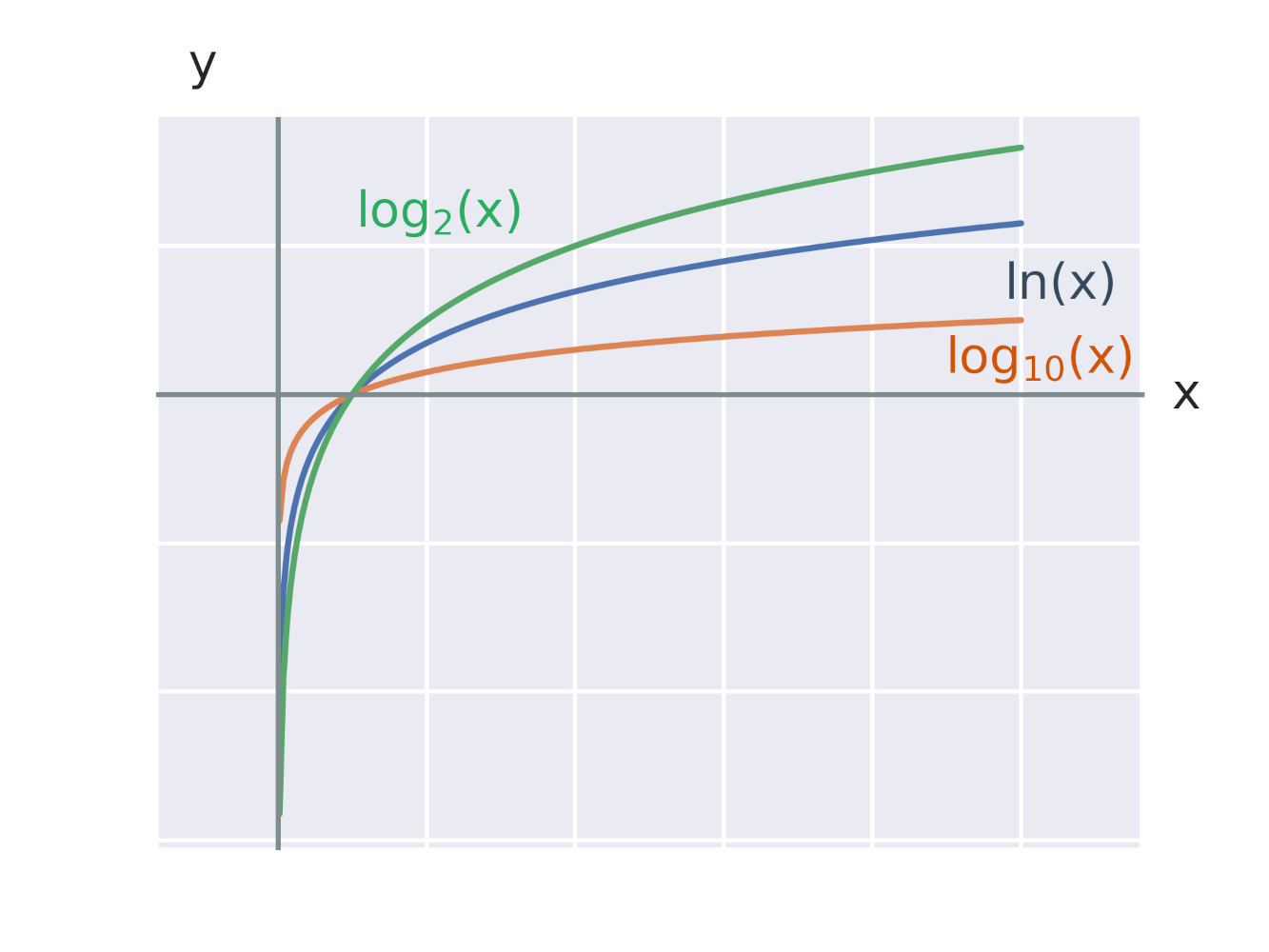
Позначення деяких визначних логарифмічних функцій:
| функція | опис | інші можливі позначення |
|---|---|---|
| \log_a x | загальний логарифм x з основою a для будь-якого a >0, a\neq 1 | |
| \ln x | натуральний логарифм x, тобто логарифм x з основою e | в англійських текстах іноді \log x |
| \log x | десятковий логарифм x, тобто логарифм x з основою 10 | \log_{10}x |
| \log_2 x | бінарний логарифм x, тобто логарифм x з основою 2 | іноді зустрічається \mathrm{lb}\;x |
Ефект додавання константи до логарифмічної функції
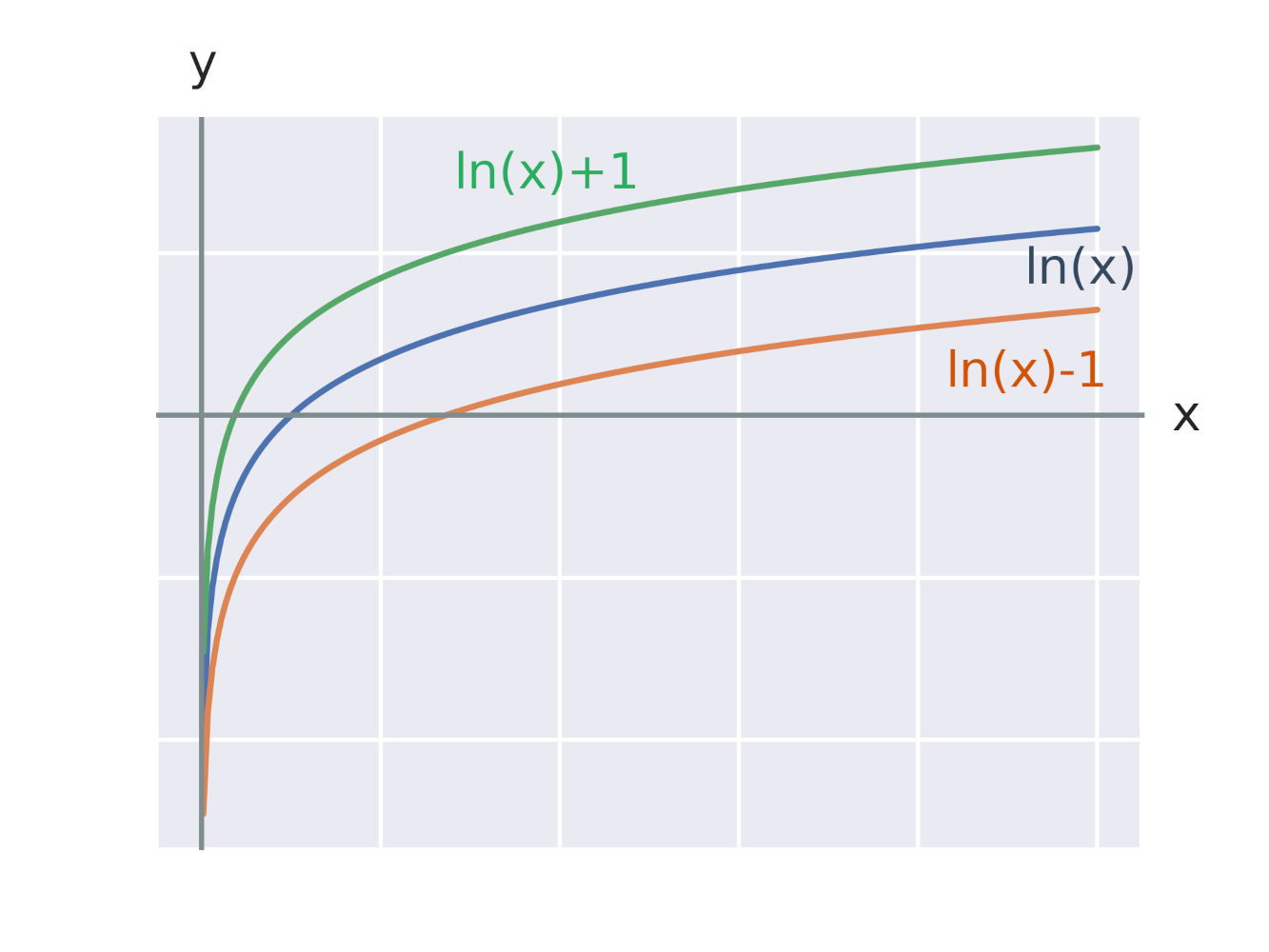
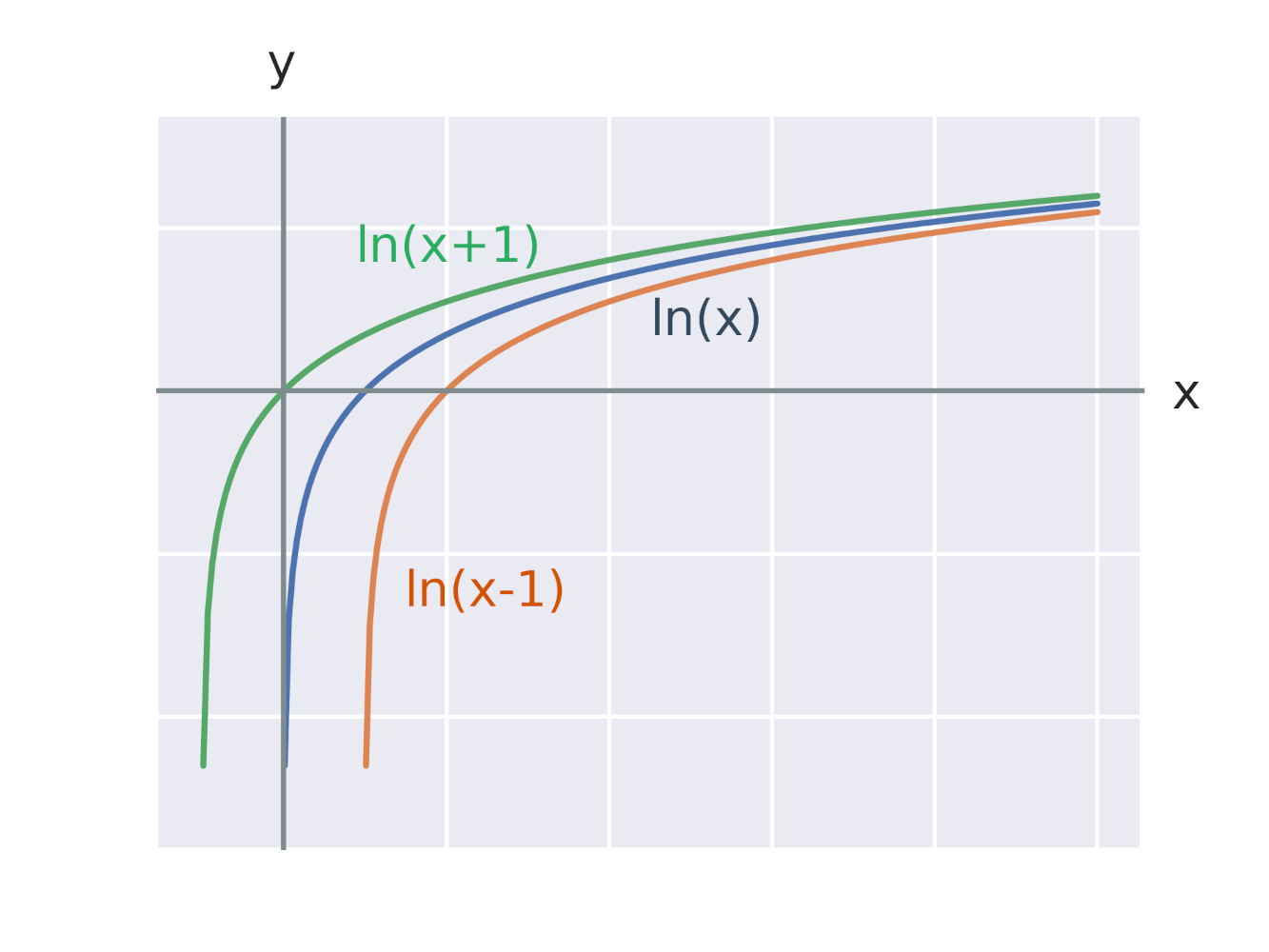
Ефект додавання константи до аргументу логарифмічної функції
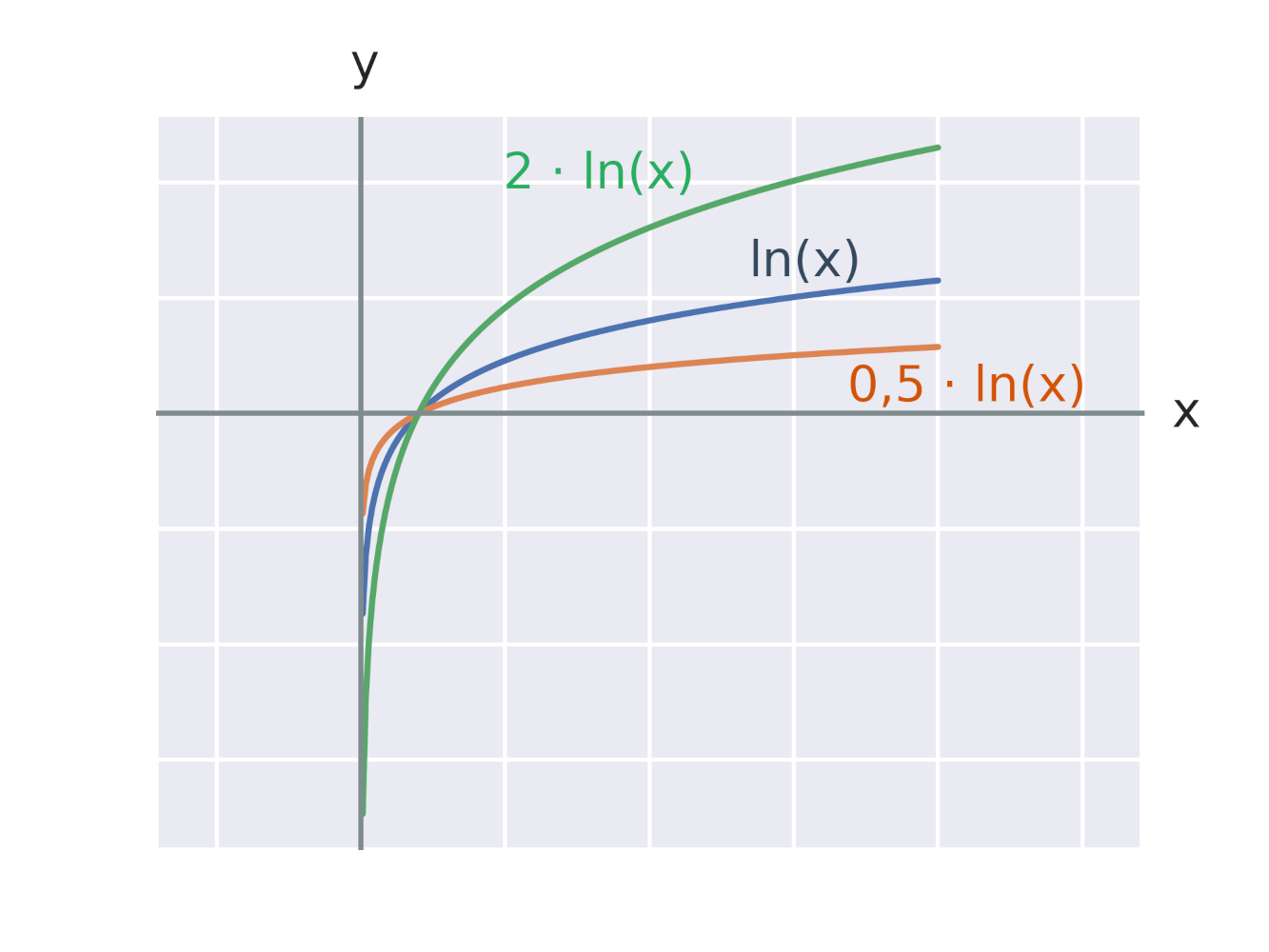
Ефект множення логарифмічної функції на константу
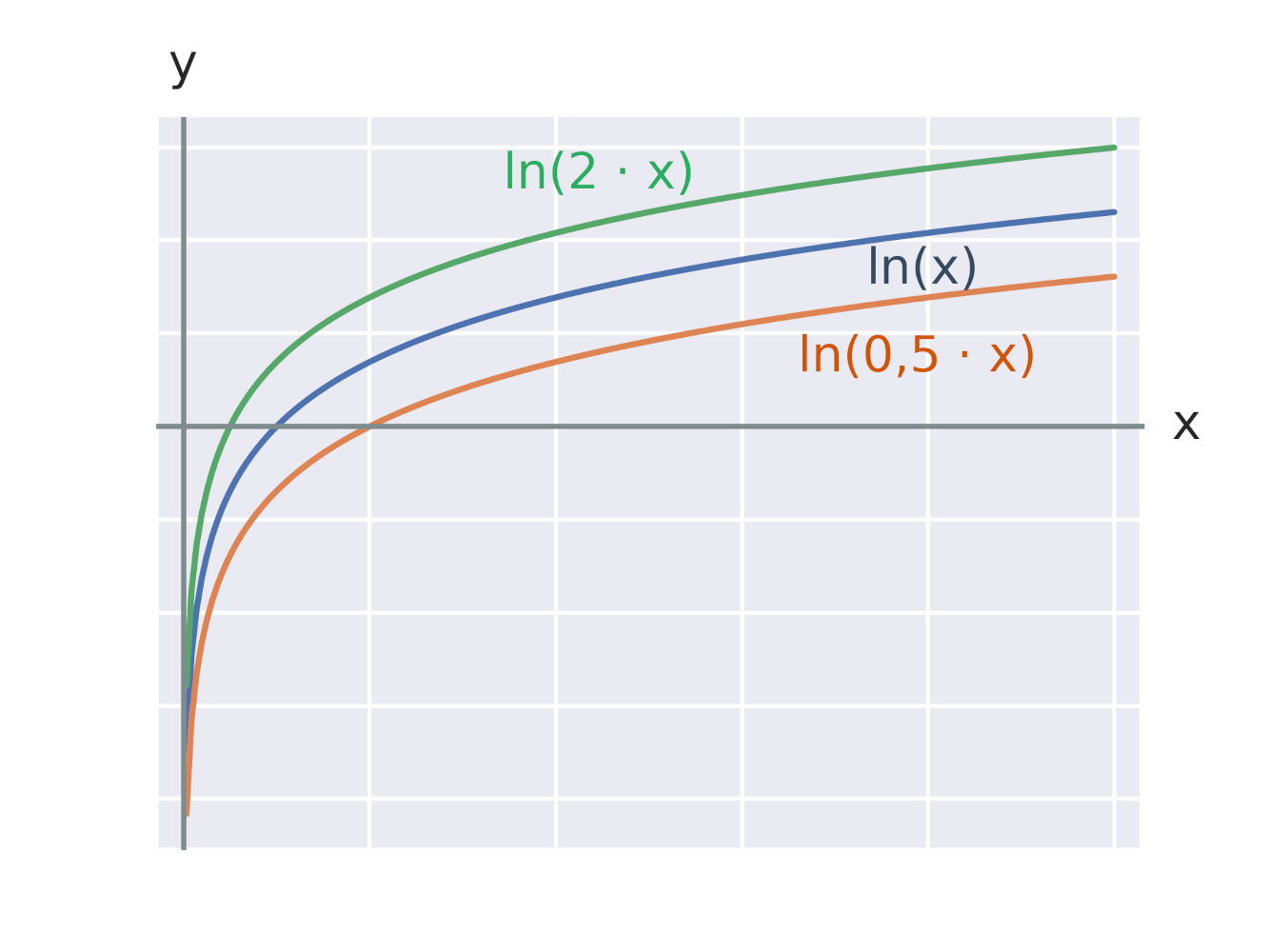
Ефект множення аргументу логарифмічної функції на константу
Переміщення
Переміщення карт на правильне місце. Просте управління, цікаві та оригінальні завдання.
Вибір
Швидке практикування шляхом вибору з двох варіантів.
Графікобудівник
Спеціалізовані вправи для роботи з графіками та функціями.