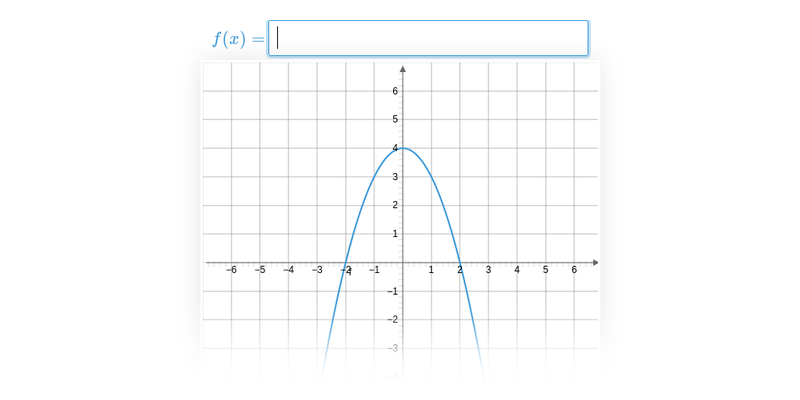
Графіки квадратичних функцій

Квадратичну функцію можна виразити у вигляді f(x) = ax^2 + bx + c, де a\neq 0. Графіком квадратичної функції є парабола. Цей графік зображує функцію 0{,}5 x^2 + x - 4:

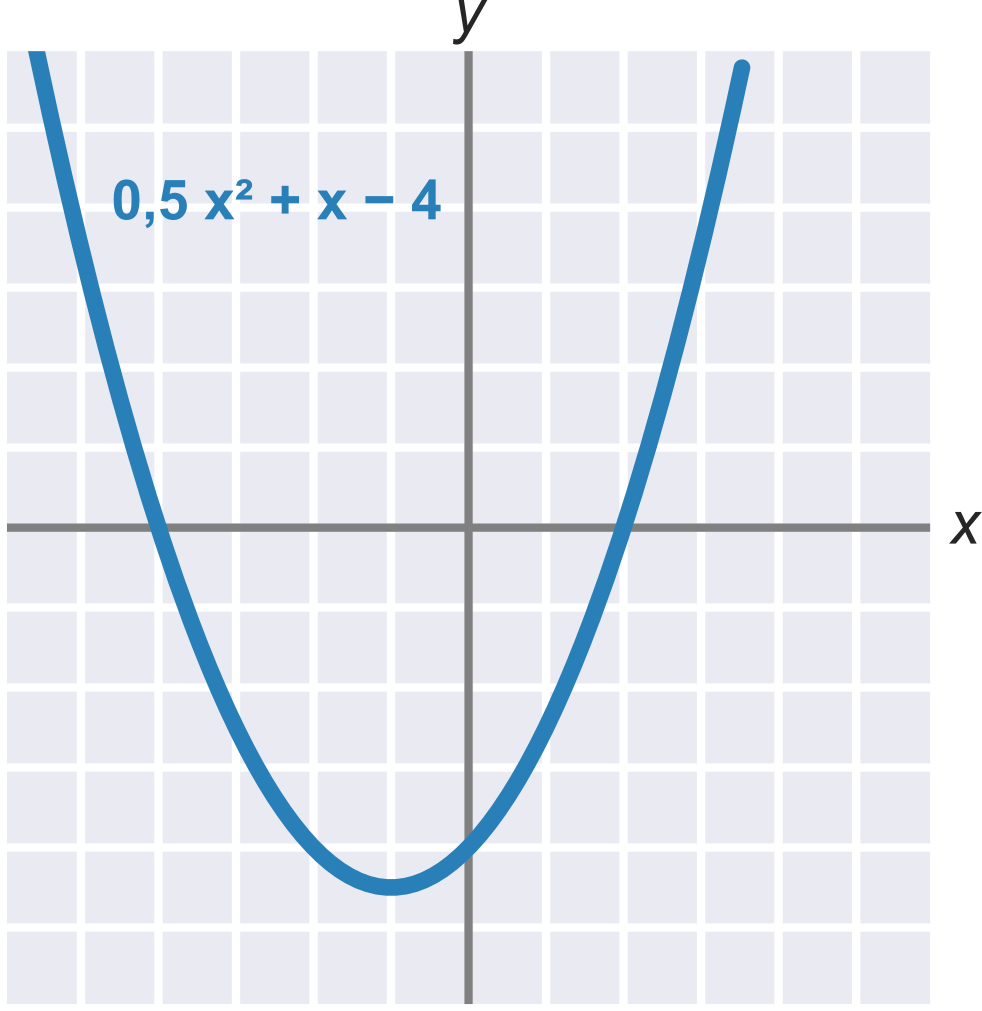
Точки перетину з віссю x є розв’язками квадратного рівняння ax^2 + bx + c = 0. Для наведеного прикладу 0{,}5 x^2 + x - 4 цими розв’язками є x_1 = -4 a x_2 = 2.

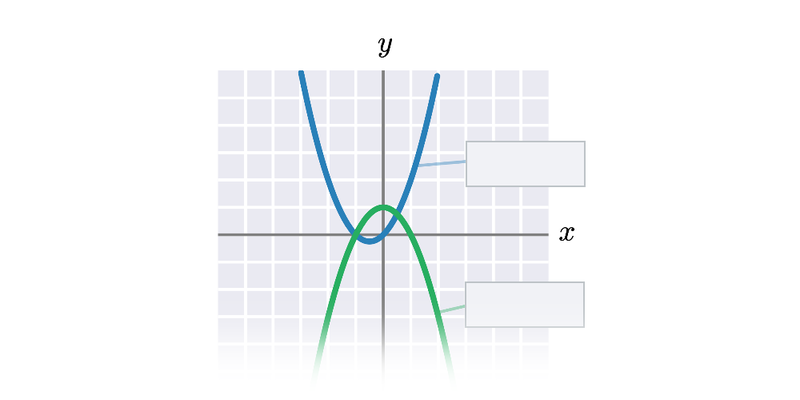
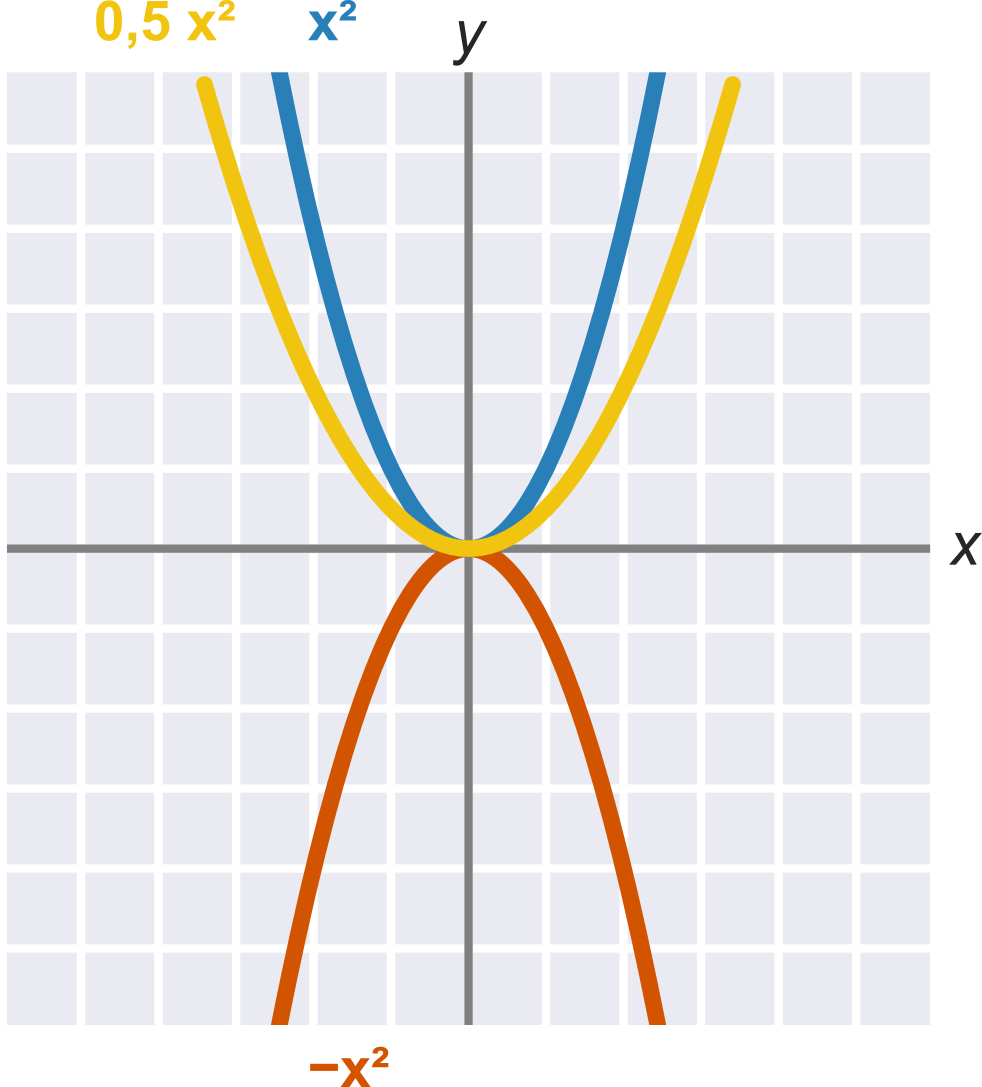
Квадратичний коефіцієнт a впливає на основну форму параболи:

Якщо a>0, «парабола спрямована вгору» (точніше: це функція, обмежена знизу, опукла).
Якщо a<0, «парабола спрямована вниз» (точніше: це функція, обмежена згори, увігнута).
Розмір квадратичного коефіцієнта a впливає на те, наскільки «широка» парабола.

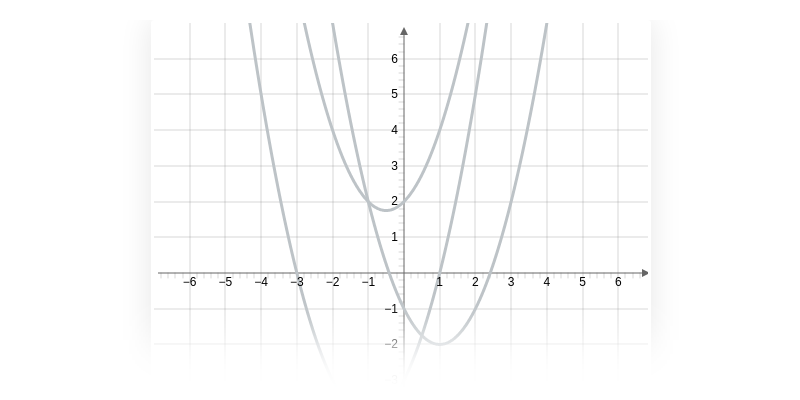
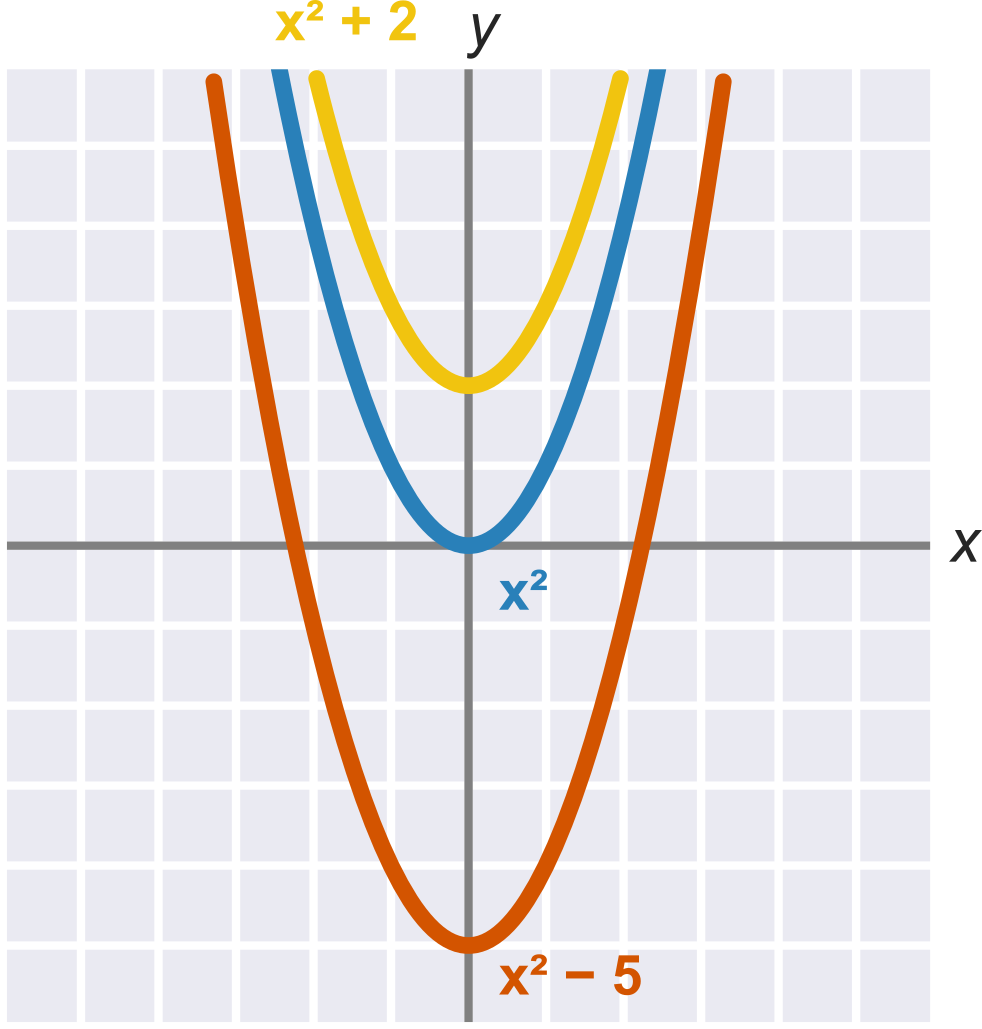
Константний член c впливає на зміщення параболи – він вказує на точку перетину з віссю y.

Переміщення

Переміщення карт на правильне місце. Просте управління, цікаві та оригінальні завдання.

Графіки квадратичних функцій

Пошук вершини параболи: піднесення до квадрата

Графіки квадратичних функцій

Переміщення • складне

Графіки квадратичних функцій

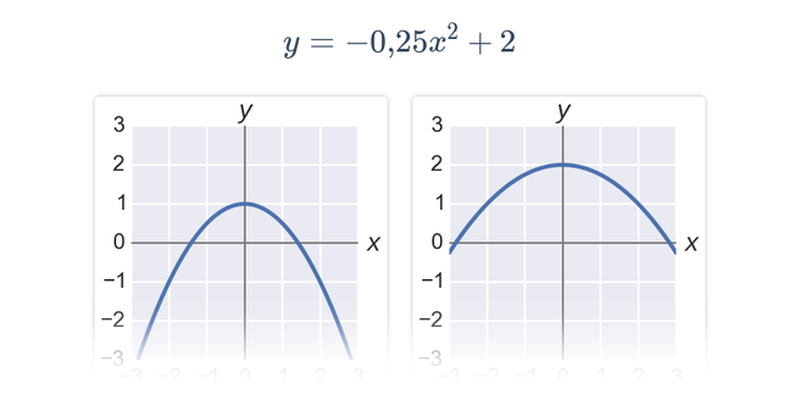
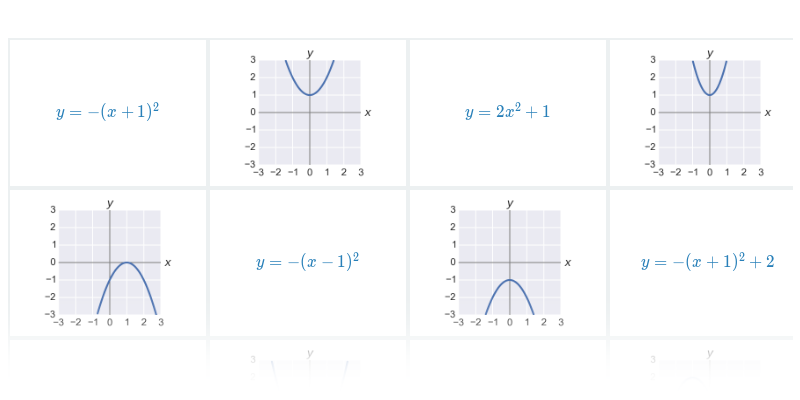
Вибір

Швидке практикування шляхом вибору з двох варіантів.

Графіки квадратичних функцій

Графіки квадратичних функцій

Вибір • складне

Графіки квадратичних функцій

Pexeso

Вправа на знаходження пар.

Графіки квадратичних функцій

Графіки квадратичних функцій

Pexeso • складне

Графіки квадратичних функцій

Графікобудівник

Спеціалізовані вправи для роботи з графіками та функціями.

Графіки квадратичних функцій

Графіки квадратичних функцій

Графікобудівник • складне

Графіки квадратичних функцій

ЗВ’ЯЖІТЬСЯ З НАМИ

Дякуємо за ваше повідомлення, його було успішно відправлено.

Напишіть нам

Вам потрібна допомога?

Будь ласка, спочатку ознайомтеся з поширеними запитаннями:

Поширені запитання

Про що йдеться у повідомленні?

Повідомлення Зміст Управління Вхід до системи Ліцензія