Дякуємо за Ваш відгук.

Біноміальний коефіцієнт

Комбінаторне число вказує на кількість комбінацій, тобто способів, як вибрати k елементів із множини з n елементів. Комбінаторні числа дуже часто зустрічаються в комбінаторних обчисленнях, тому мають спеціальне позначення \binom{n}{k} (читаємо „n над k“).

Для n \geq k \geq 0 виконується формула: \binom{n}{k} = \frac{n!}{k!(n-k)!}

Для комбінаторних чисел існує ряд інших співвідношень, наприклад:

\binom{n}{k} = \binom{n}{n-k}
\binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1}
\sum_{k=0}^n \binom{n}{k} = 2^n

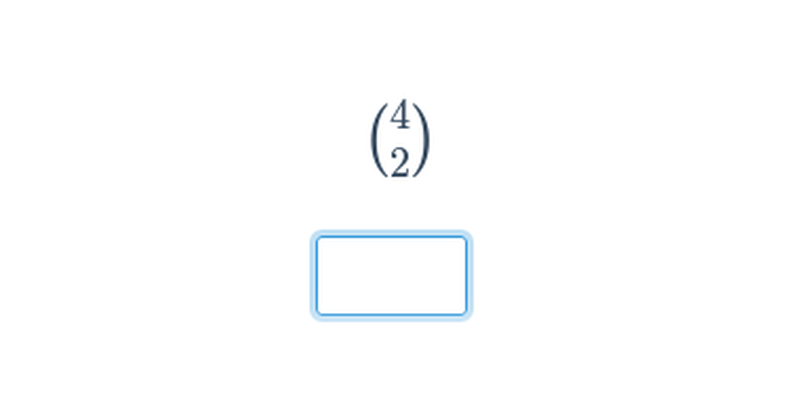
Приклади:

\binom{3}{1}	= 3
\binom{4}{2}	= 6
\binom{5}{3}	= 10
\binom{6}{2}	= 15
\binom{15}{15}	= 1

Pexeso

Вправа на знаходження пар.

Біноміальний коефіцієнт

Pexeso • складне

Письмова відповідь

Вправа, в якій ви набираєте відповідь на клавіатурі.

Біноміальний коефіцієнт

Письмова відповідь • середній

Попередній

Подальший

Вправи

Біноміальний коефіцієнт

Pexeso