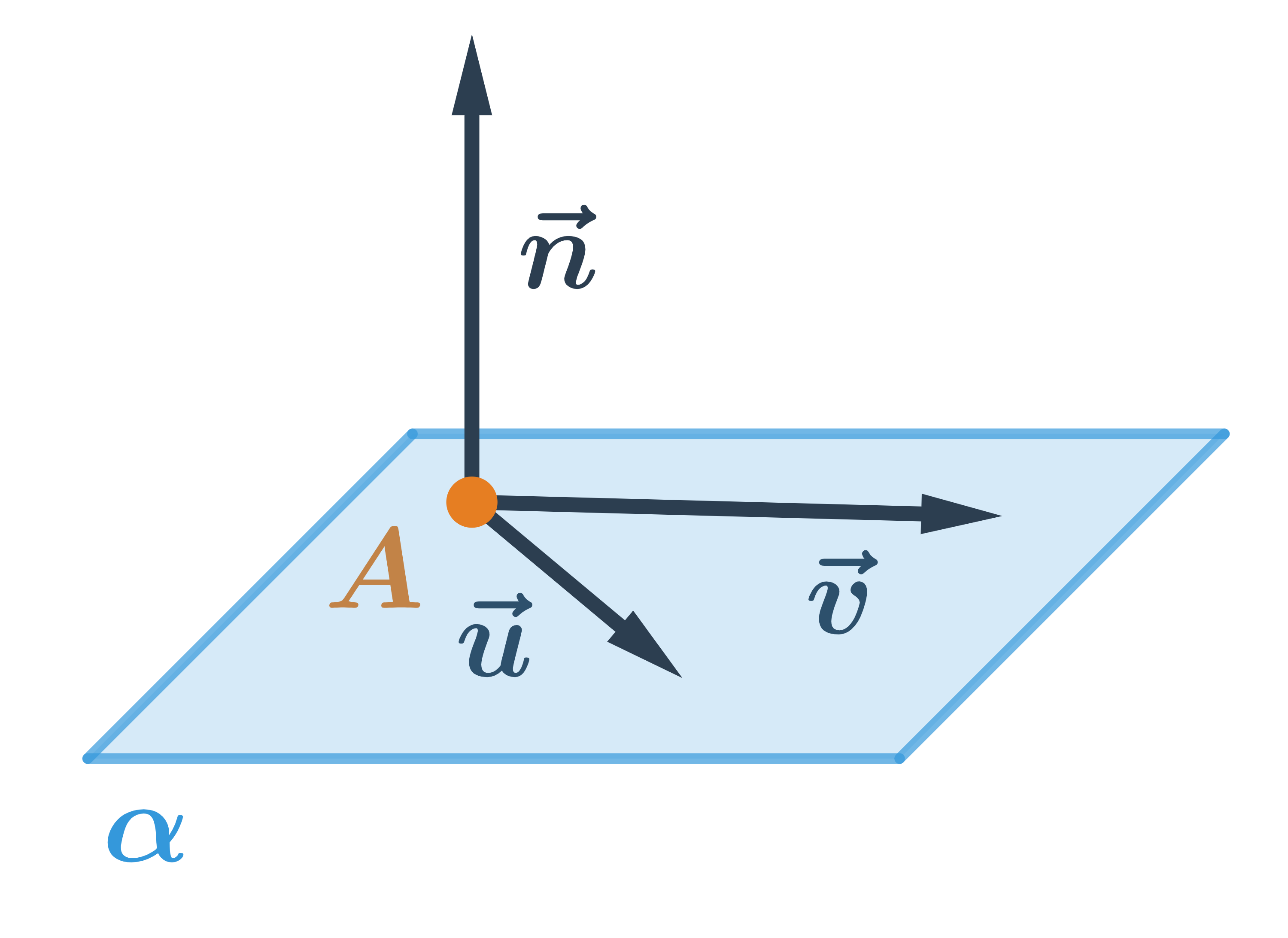
Пряма однозначно визначається точкою та двома векторами, які не є колінеарними. На малюнку площина \alpha визначена точкою A та векторами \vec{u}, \vec{v}. Кожен вектор, який є перпендикулярним до площини \alpha називається нормаллю площини \alpha. На рисунку зображено нормаль \vec{n}.
Параметричні рівняння площини
Площина, визначена точкою A=[a_1;a_2;a_3] та векторами \vec{u}=(u_1;u_2;u_3) та \vec{v}=(v_1;v_2;v_3), має параметричні рівняння такого вигляду:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Скорочено можемо записати \alpha:X=A+t\vec{u}+s\vec{v}, де t, s називаються параметрами.
Загальне рівняння площини
Загальне рівняння площини має вигляд ax+by+cz+d=0, де константи a, b, c є координатами нормалі, а d є дійсне число.
Загальне рівняння площини, паралельної осям x та y
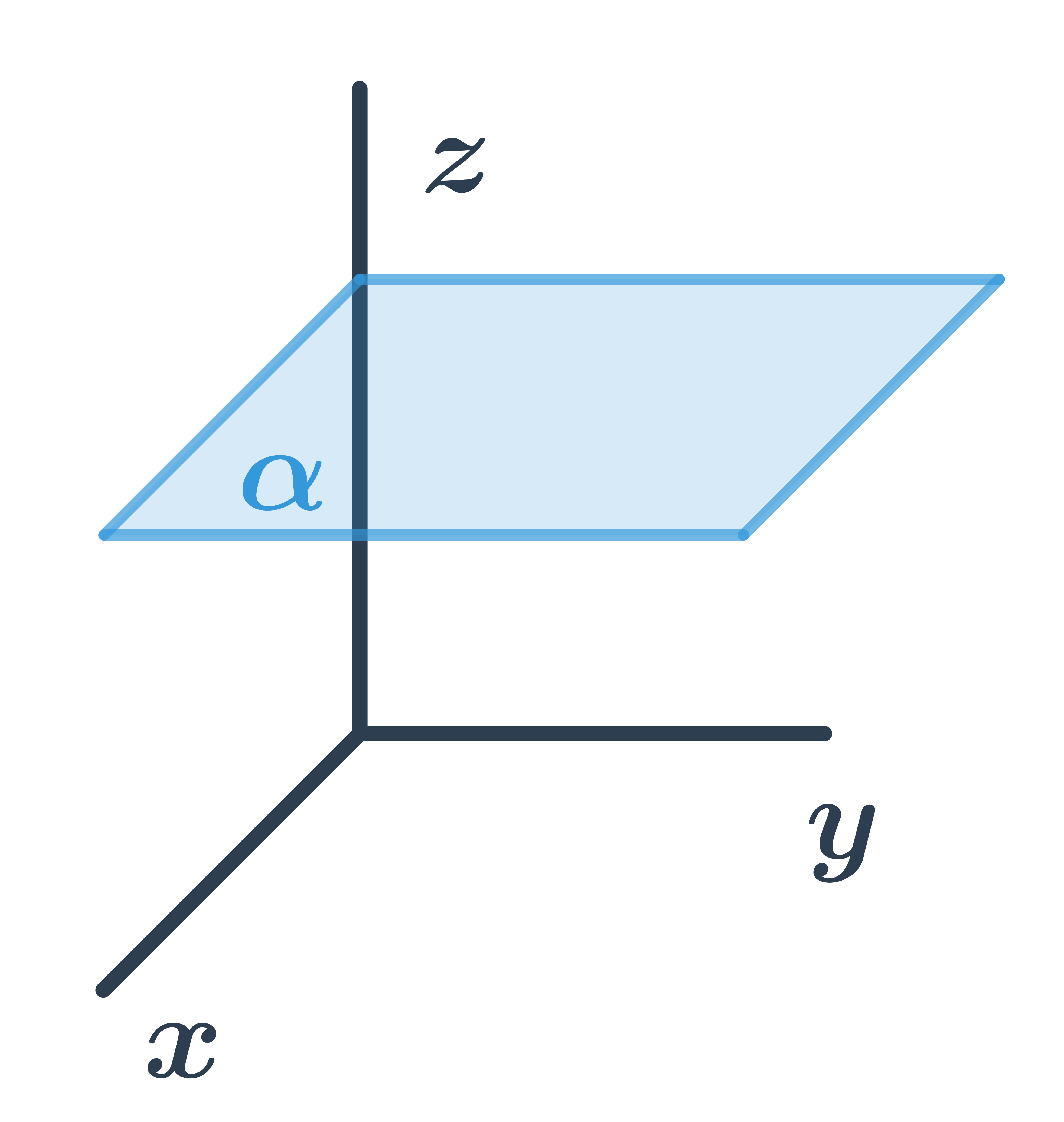
Для всіх точок, що лежать у площині, третя координата однакова, тому площина має загальне рівняння: z+d=0.
Загальне рівняння площини, паралельної осям x та z
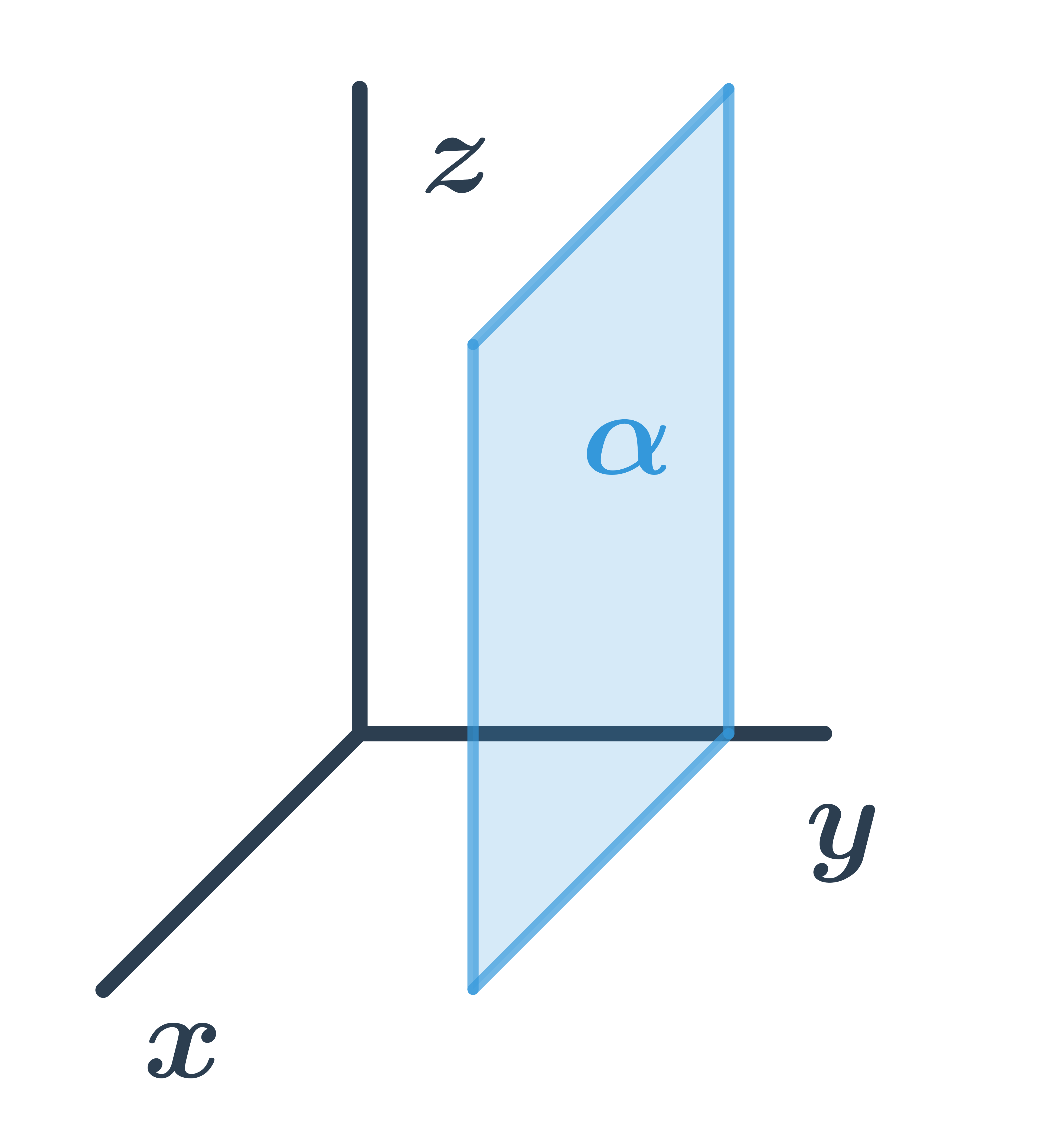
Для всіх точок, що лежать у площині, друга координата однакова, тому площина має загальне рівняння: y+d=0.
Загальне рівняння площини, паралельної осям y та z
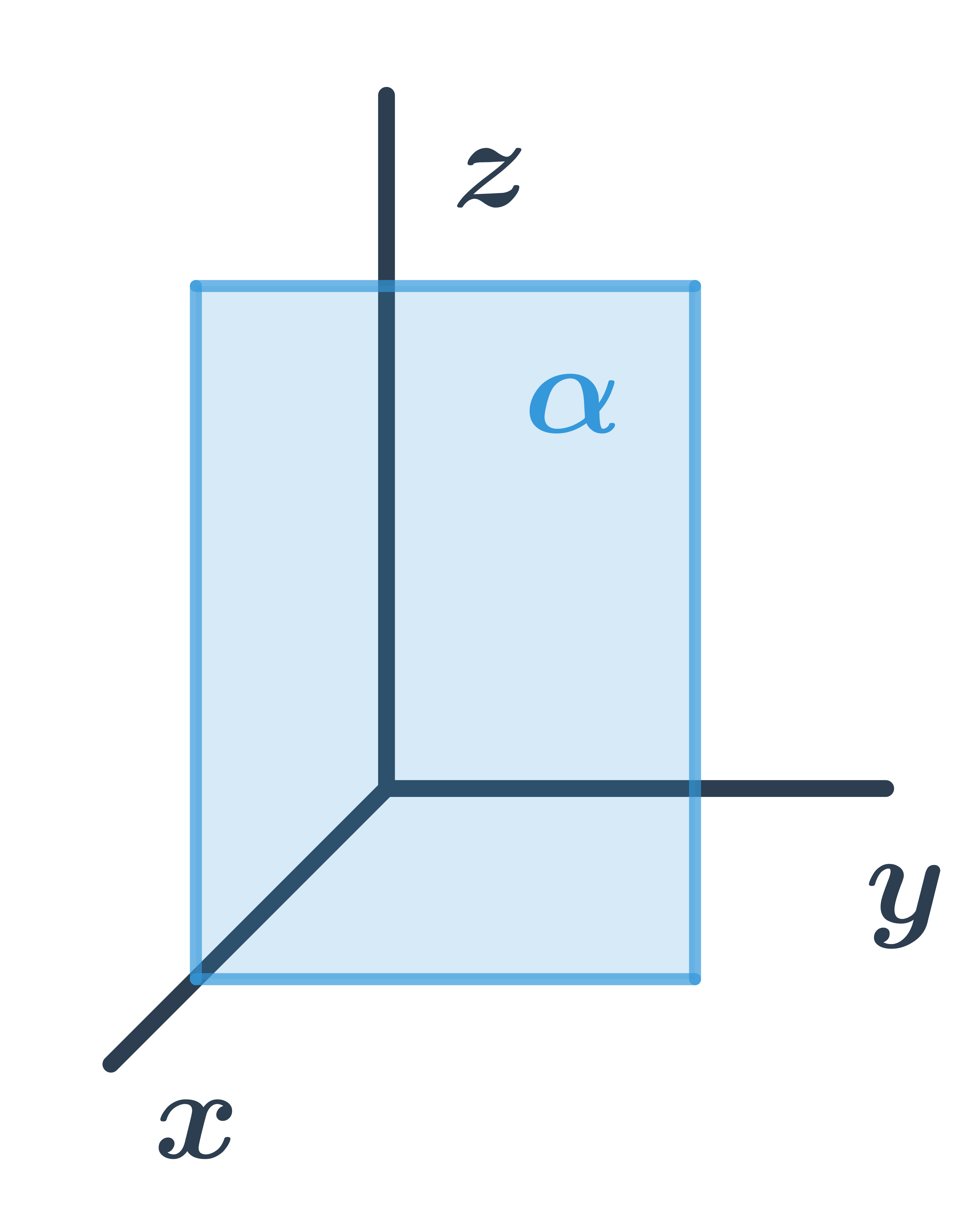
Для всіх точок, що лежать у площині, перша координата однакова, тому площина має загальне рівняння: z+d=0.
Точка та площина
Точка M=[m_1;m_2;m_3] лежить у площині, якщо її координати задовольняють рівняння площини.
- Якщо площина задана загальним рівнянням ax+by+cz+d=0, для координат точки, яка лежить на прямій, виконується рівність: a\cdot m_1+b\cdot m_2+c\cdot m_3+d=0
- Якщо площина задана параметрично, то після підстановки координат точки у параметричні рівняння отримуємо систему трьох рівнянь з двома невідомими t, s, яка має єдине розв’язання (пару дійсних чисел).
Загальне рівняння площини, яка проходить через початок координат
- Площина проходить через точку O=[0;0;0], отже, має виконуватися рівність: a\cdot0+b\cdot0+c\cdot0+d=0\Rightarrow d=0.
- Площина, яка проходить через початок координат, має загальне рівняння: ax+by+cz=0.
Дві паралельні площини
Нормалі двох паралельних площин \alpha: a_1x+b_1y+c_1z+d_1=0 a \beta: a_2x+b_2y+c_2z+d_2=0 є колінеарними, тобто координати одного вектора є кратними координатам іншого вектора. Для констант у загальних рівняннях має виконуватися:
\begin{array}{rll}a_2&=&k\cdot a_1\\ b_2&=&k\cdot b_1\\c_2&=&k\cdot c_1\\&&k\in\mathbb{R}\end{array}
Якщо також виконується рівність d_2=k\cdot d_1, то площини є тотожними.













