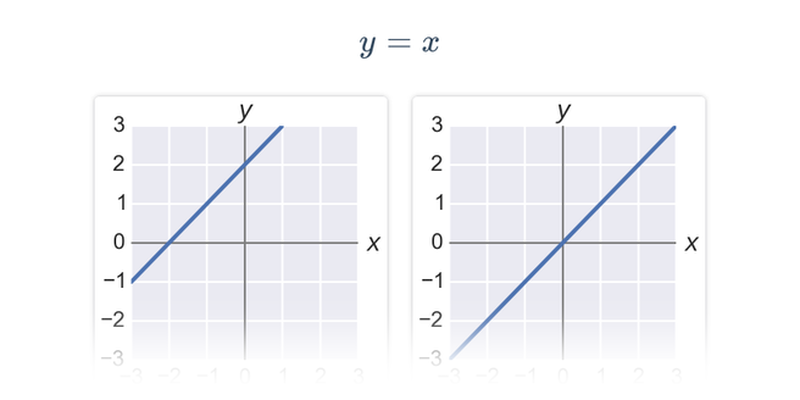
Лінійні функції
Функція f є лінійною, якщо її можна виразити у вигляді f(x) = a\cdot x + b, де a і b є константами. Графіком лінійної функції є пряма. Параметр a є коефіцієнтом нахилу (також називається кутовим коефіцієнтом), параметр b визначає її вертикальне зміщення (також називається вільним членом).
Приклади лінійних функцій:
- f(x) = 2x
- f(x) = -4x+8
- f(x) = \frac13 x + 1{,2}
Щоб функція була лінійною, не обов’язково, щоб вона була записана безпосередньо у вигляді f(x) = a\cdot x + b. Достатньо, щоб її можна було привести до цього вигляду. Приклади:
- f(x) = 2-x можна переписати як f(x)= -1x + 2, що є лінійною функцією з коефіцієнтом нахилу -1 і вільним членом 2.
- f(x) = 5(3-x) можна переписати як f(x)= -5x + 15, що є лінійною функцією з коефіцієнтом нахилу -5 і вільним членом 15.
- f(x) = x^2 + 7 - x(x-1) на перший погляд виглядає як квадратична функція, але її можна привести до вигляду f(x)= x + 7 (квадратичний член зникає), тож це лінійна функція.
Вибір
Швидке практикування шляхом вибору з двох варіантів.