Кути та окружність

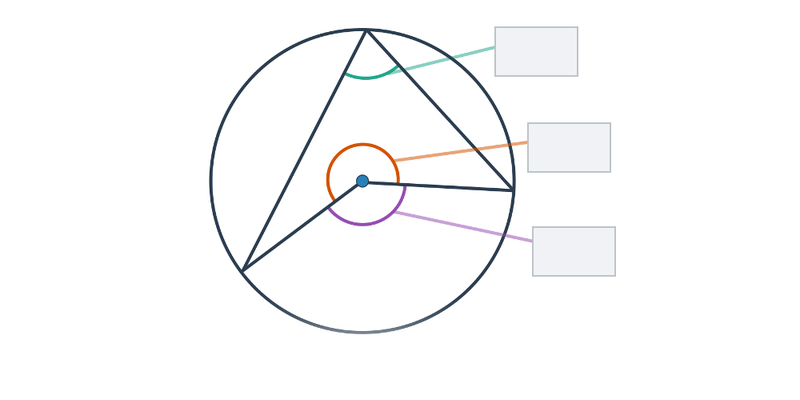
Центральний кут

Кут з вершиною в центрі S кола k, сторони якого проходять через крайні точки A, B дуги кола k.
Для будь-яких двох точок на колі можна визначити два центральні кути. Кожен з них відповідає тій дузі, яка лежить у цьому куті.

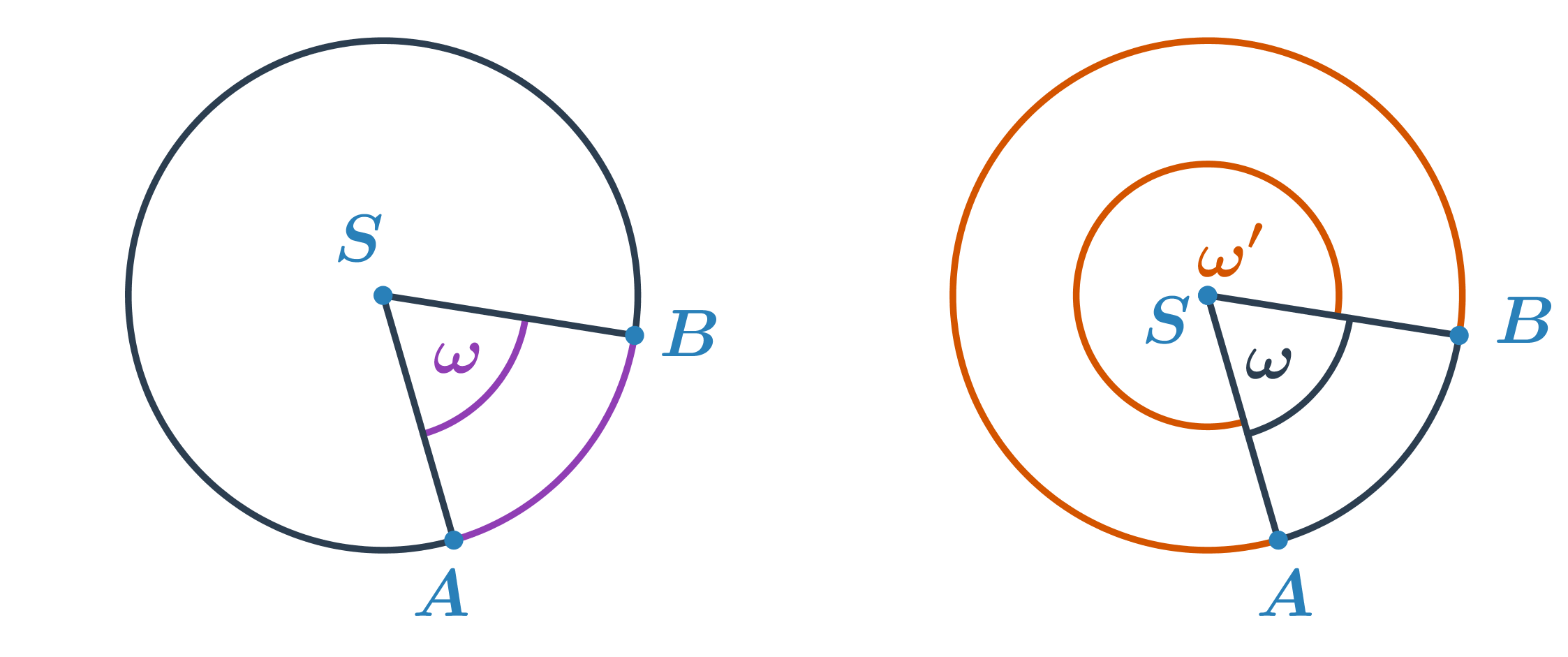
Вписаний кут

Кут, вершина V якого лежить на колі k, а сторони проходять через точки A та B дуги кола k (A \neq V \neq B)
Усі вписані кути, що відповідають дузі AB з вершиною V, яка не лежить на дузі, мають однакову величину.
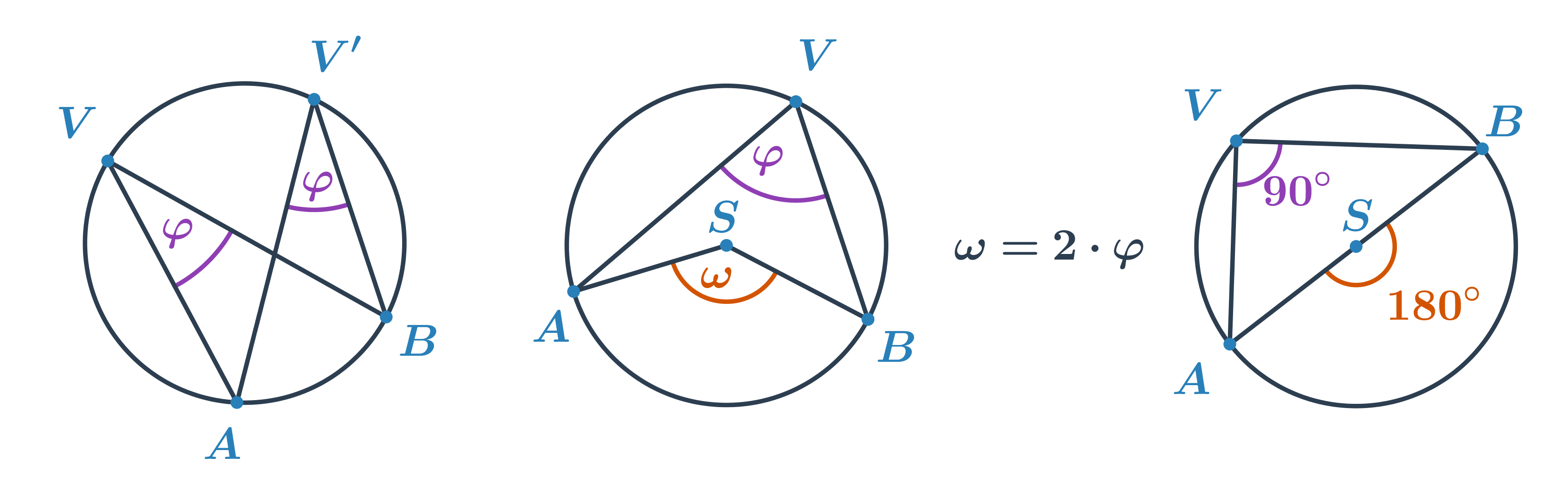
Величина центрального кута \omega дорівнює подвійному значенню вписаного кута \varphi що відповідає тій самій дузі, \omega = 2\cdot\varphi.
Теорема Фалеса: Вписаний кут, побудований на діаметрі кола, є прямим.

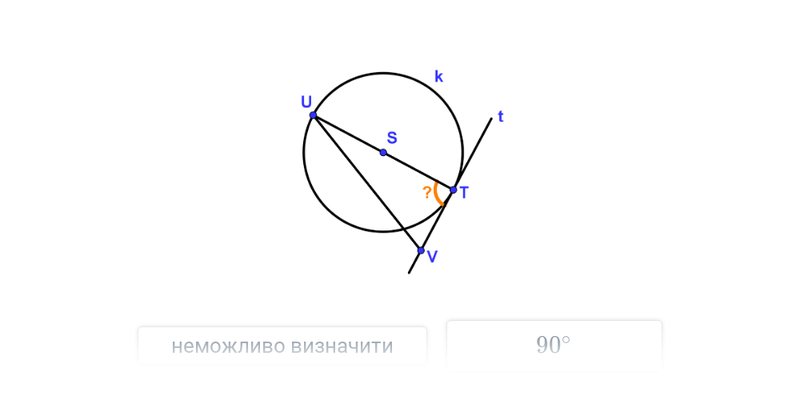
Січний кут

Кут, який утворюється хордою AB кола k з дотичною t до кола в точці A або B.
Величина січного кута дорівнює величині вписаного кута над дугою AB.

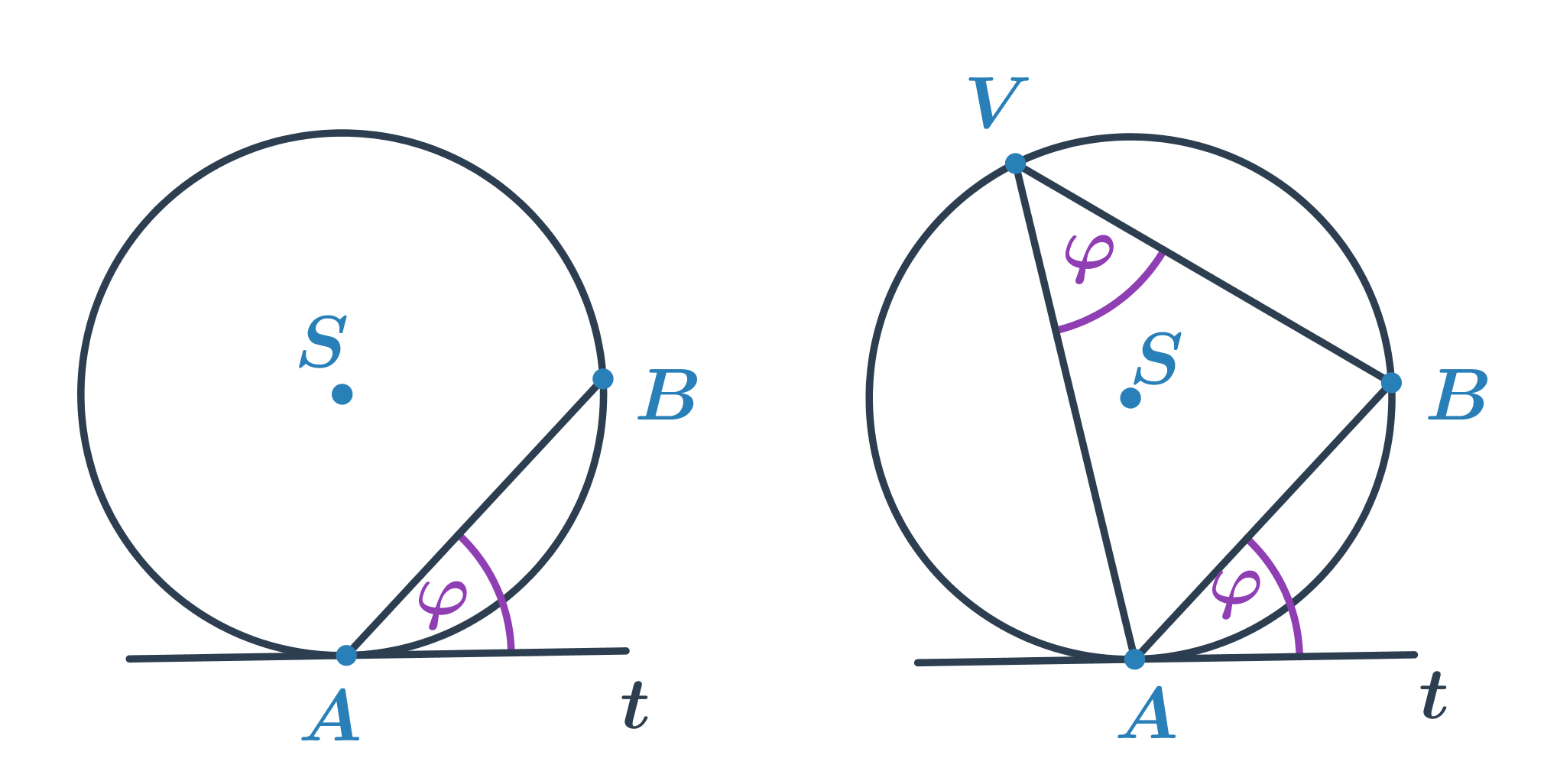
Приклад 1: Обчисліть величину оранжевого кута.

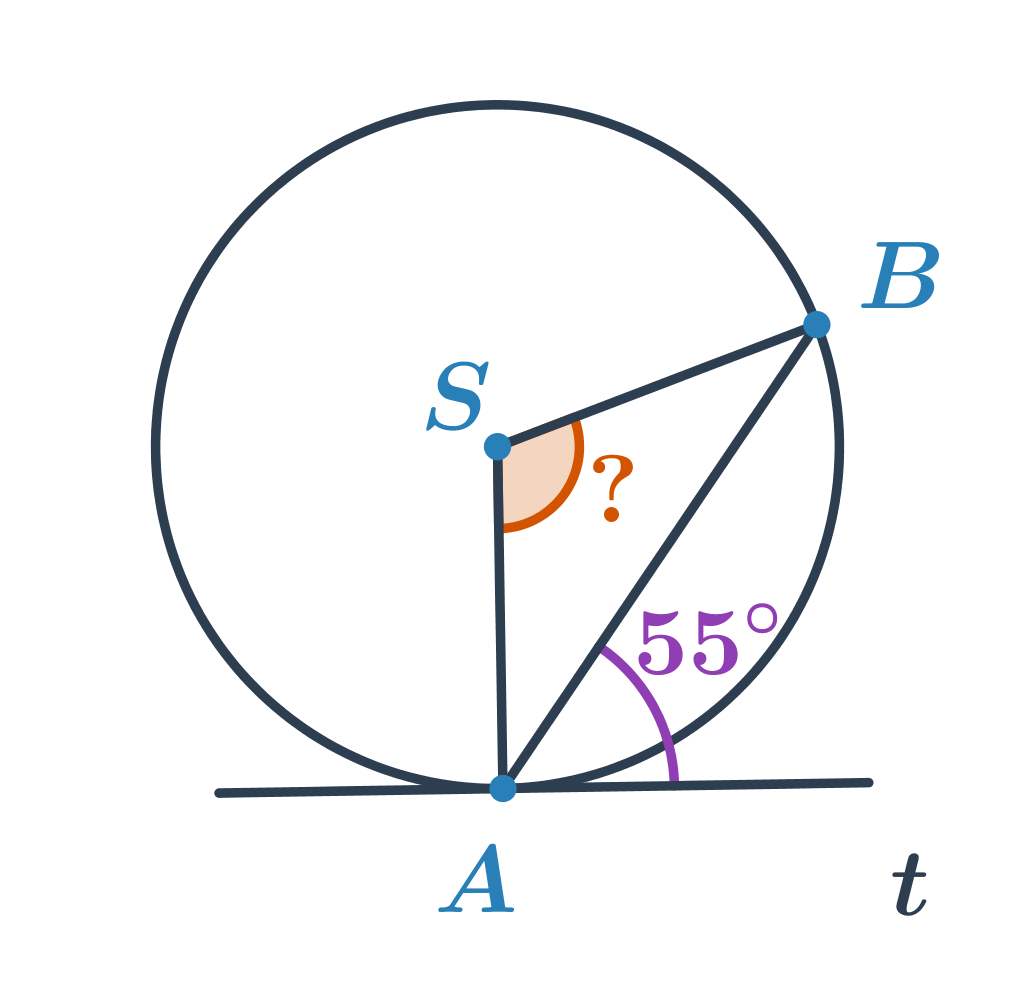
Кут величиною 55^\circ є січним кутом, що відповідає хорді AB. Відомо, що величина січного кута та відповідного вписаного кута однакові, тобто 55^\circ. Невідомий кут — це центральний кут, що відповідає меншій дузі AB. Його величина вдвічі більша за величину вписаного кута, тобто 2\cdot55^\circ=110^\circ.

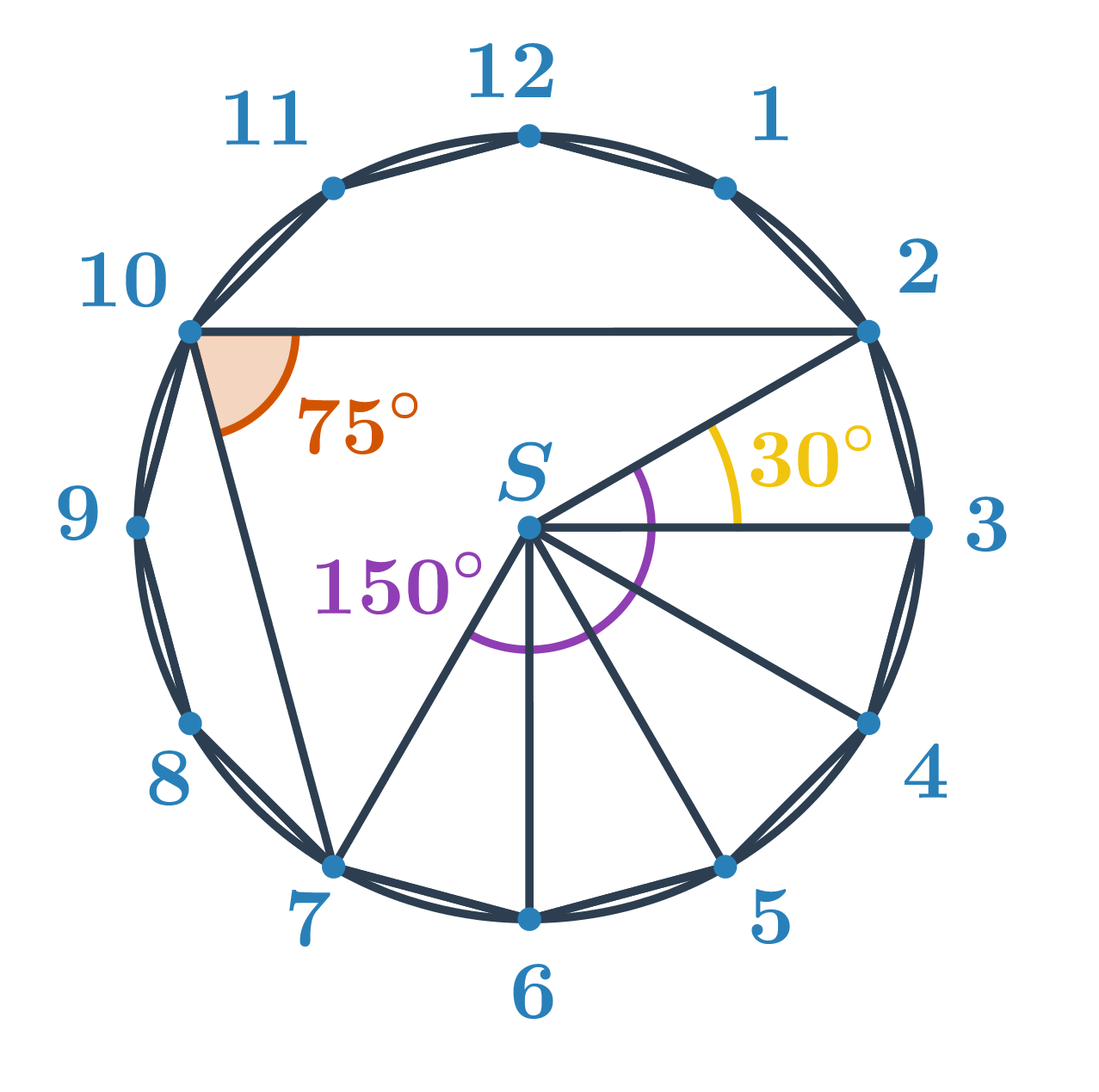
Приклад 2: Обчисліть величину оранжевого кута.

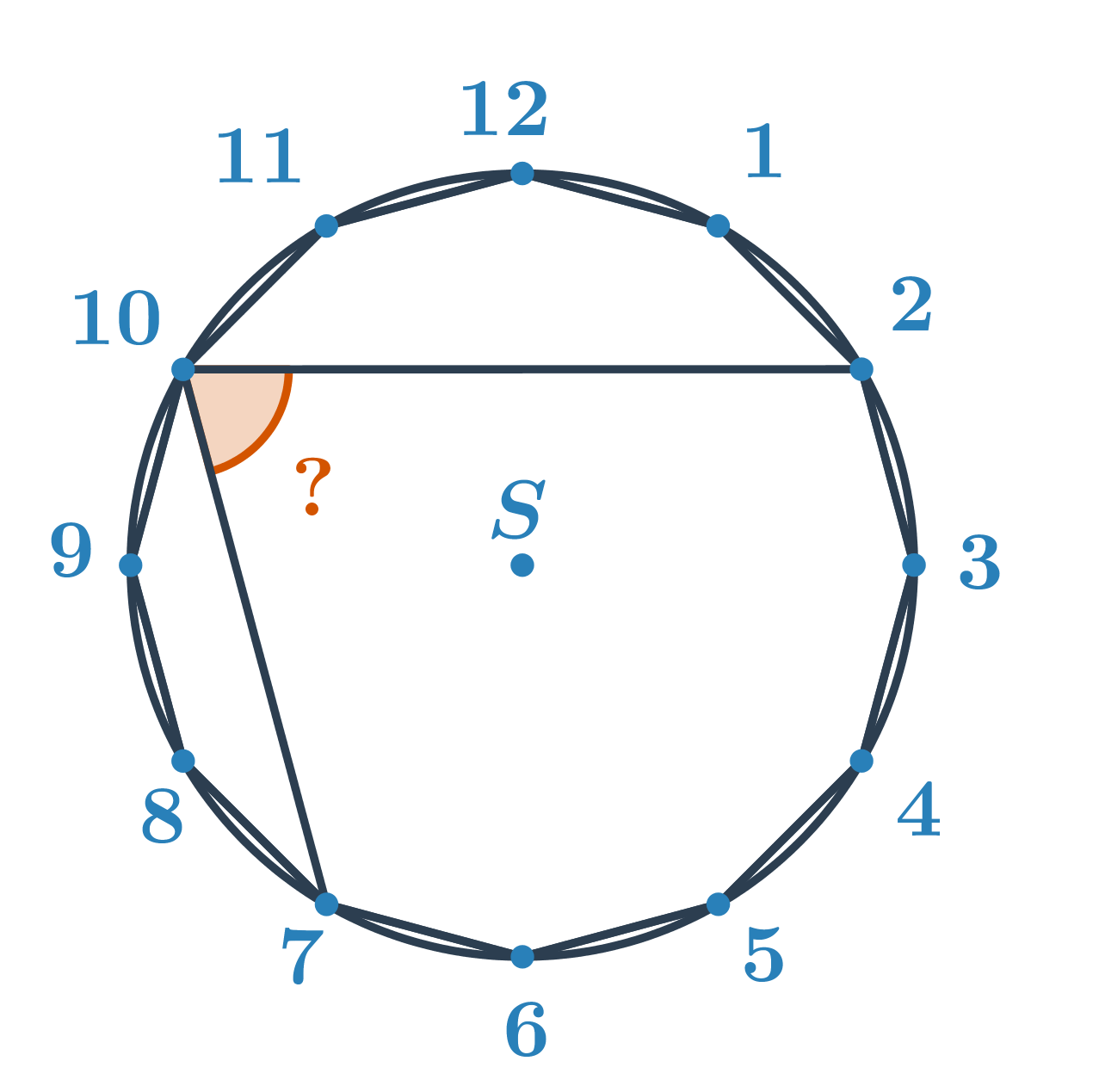
Невідомий кут є вписаним кутом над меншою дугою з кінцевими точками 2 і 7. Визначимо величину відповідного центрального кута. З розділу кути і багатокутники відомо, що величина центрального кута правильного n-кутника становить \frac{360^\circ}{n}. Таким чином, для правильного дванадцятикутного трикутника кут між двома бічними вершинами і центром дорівнює \frac{360^\circ}{12}=30^\circ. Центральний кут, відповідний дузі 2 і 7, дорівнює 5\cdot30^\circ=150^\circ. Шуканий вписаний кут має удвічі меншу величину, тобто 150^\circ:2=75^\circ.

Невідомий кут є вписаним кутом над меншою дугою з кінцевими точками 2 і 7. Визначимо величину відповідного центрального кута. З розділу кутів і багатокутників відомо, що величина центрального кута правильного n-кутника становить \frac{360^\circ}{n}. Для правильного дванадцятикутника кут між сполуками двох сусідніх вершин і центром дорівнює \frac{360^\circ}{12}=30^\circ. Центральний кут, що відповідає дузі 2 і 7, дорівнює 5\cdot30^\circ=150^\circ. Шукана величина вписаного кута вдвічі менша, тобто 150^\circ:2=75^\circ.

Переміщення

Переміщення карт на правильне місце. Просте управління, цікаві та оригінальні завдання.

Кути та окружність

Переміщення • середній

Вибір

Швидке практикування шляхом вибору з двох варіантів.

Кути та окружність

Вибір • середній

Попередній

Подальший

Вправи

Кути та окружність

Центральний кут

Вписаний кут

Січний кут

Переміщення