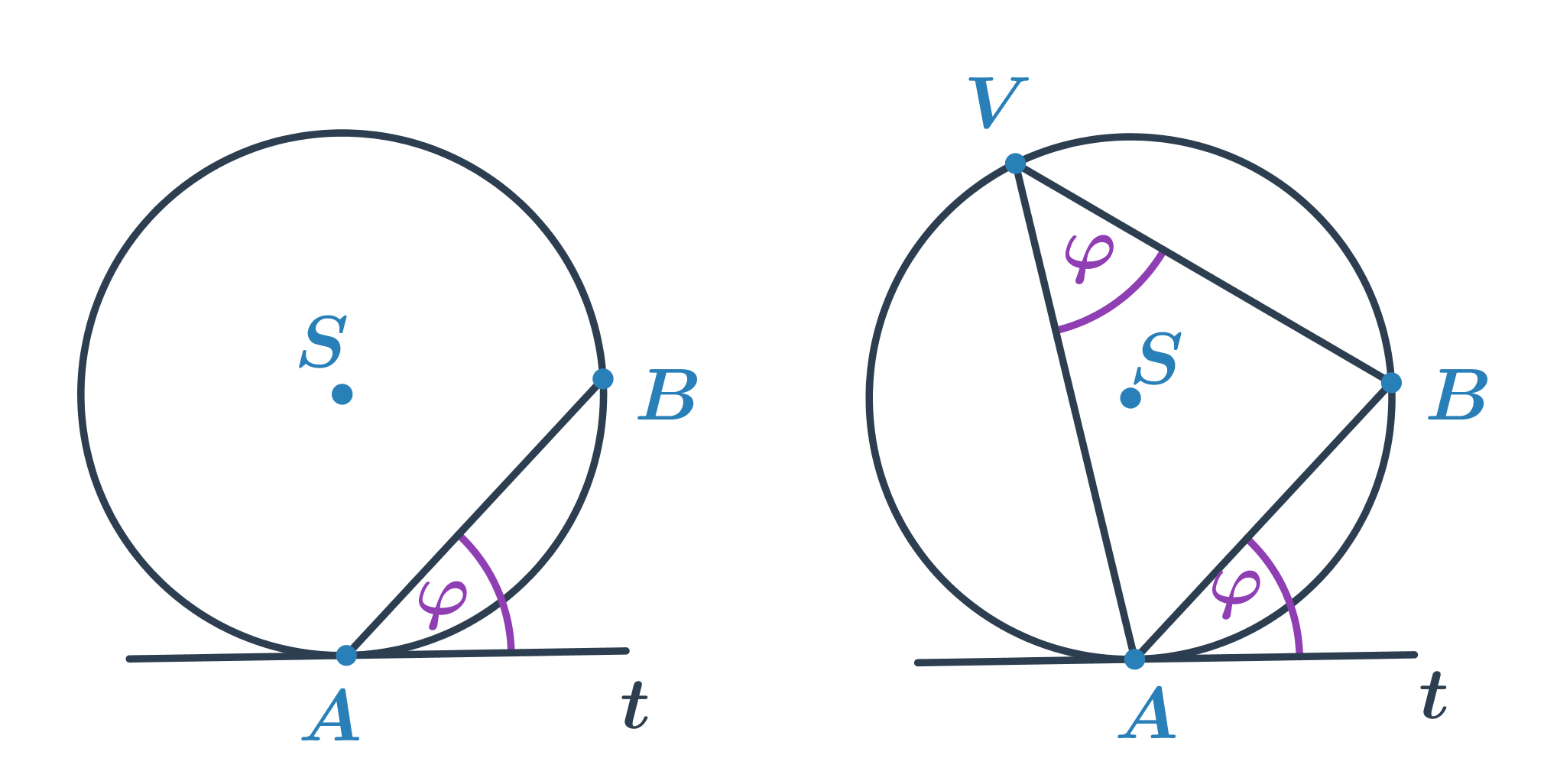Чудово, щита %% досягнуто
Кути та окружність » Вибір »
Перейти до теми:
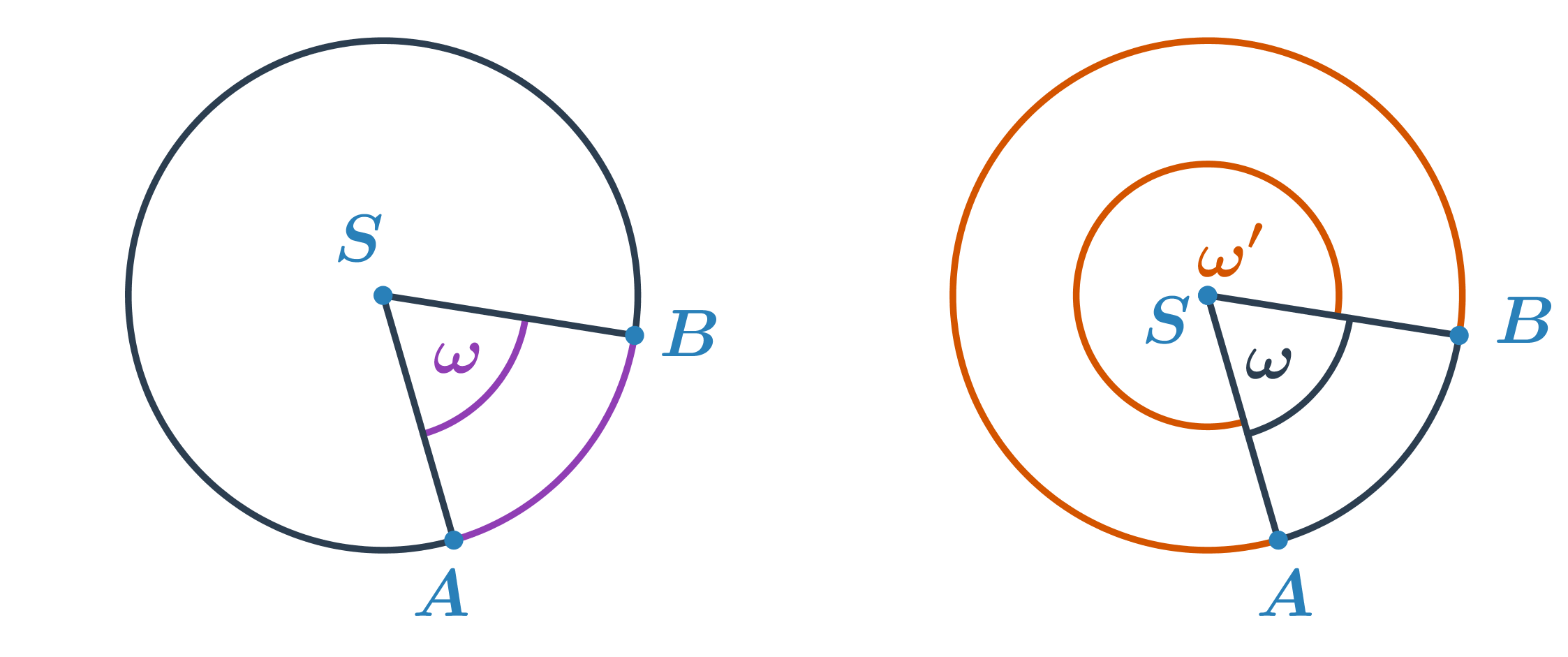
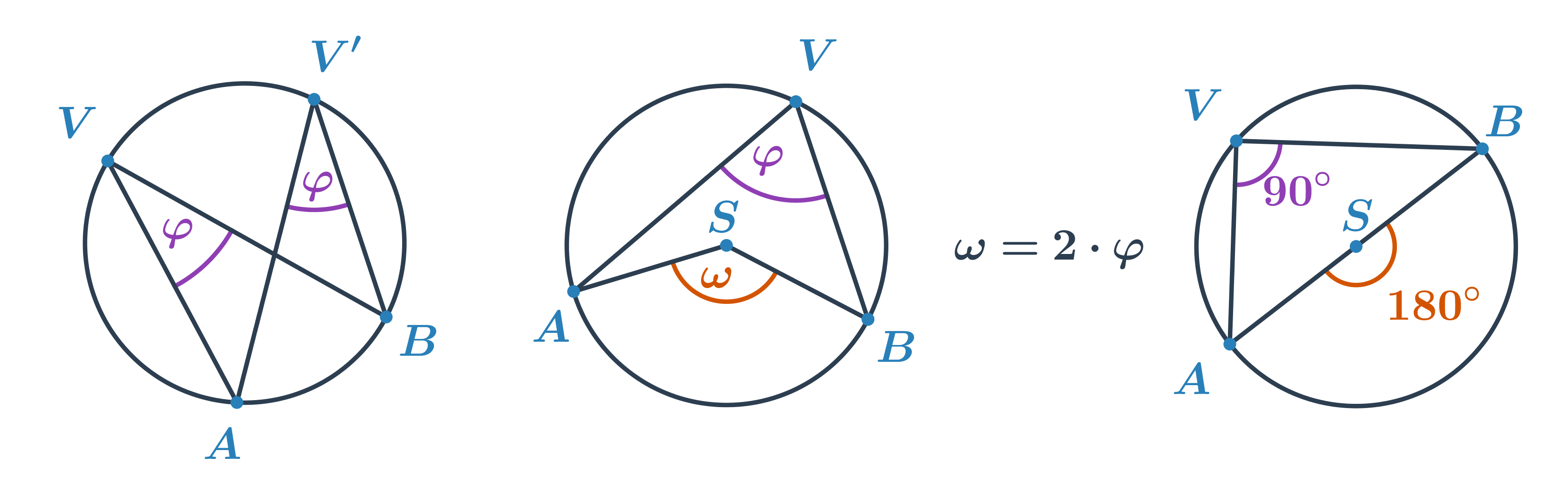
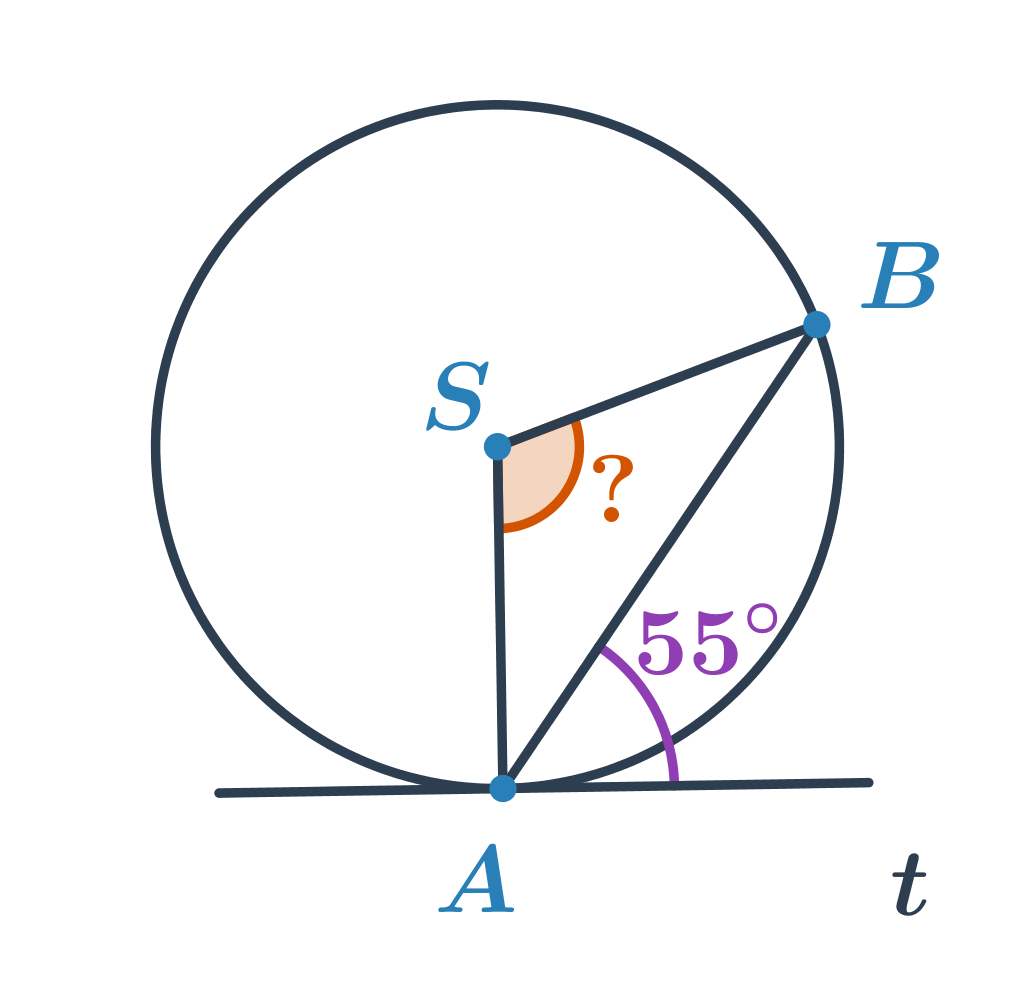
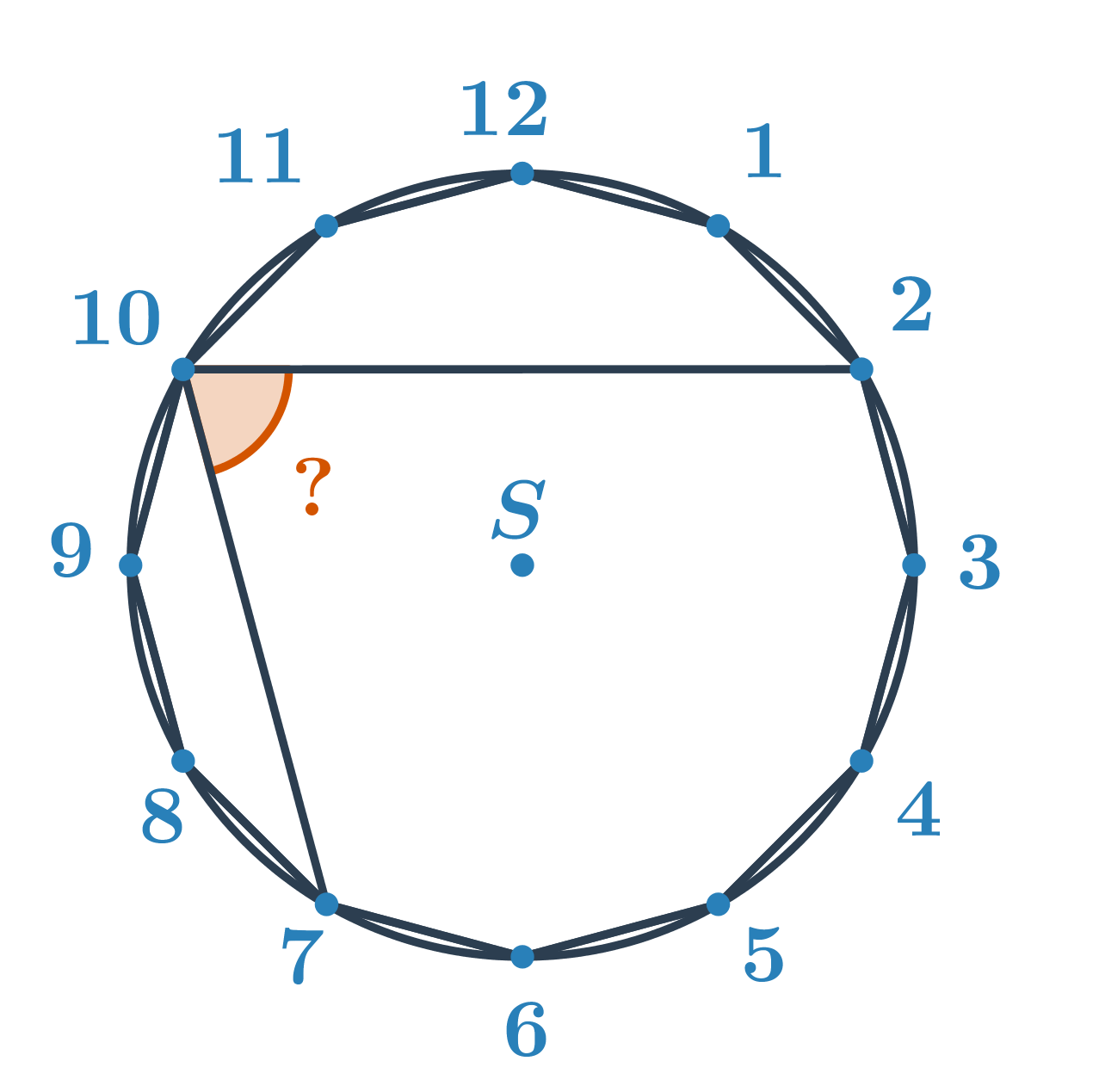
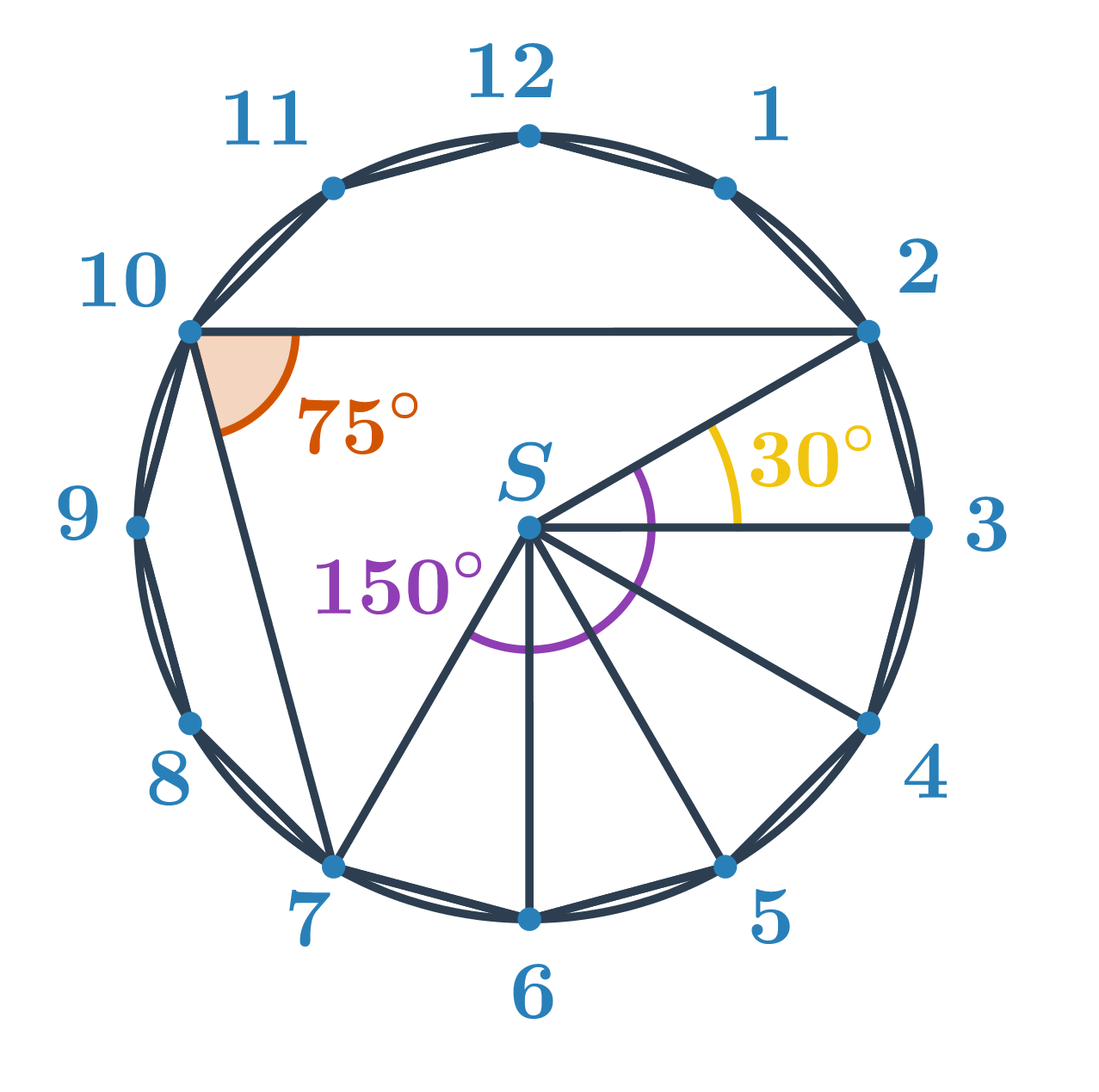
Кути та окружність
Кути та окружність
Перейти до вправи:
Вибір
Вибір
Розгорнути на весь екран
Переглянути підсумовування теми
Поділитися
Показати налаштування вправи
QR-код
QR-код можна відсканувати, наприклад, за допомогою мобільного телефону, щоб перейти безпосередньо до цієї вправи або набору прикладів.
Код / коротка адреса
Трисимвольний код можна ввести в рядок пошуку, він також є частиною скороченої адреси.
Скопіюйте, клацнувши.
FK2
Налаштування вправи
Зверніть увагу, що налаштування дійсні лише для цієї вправи та предмету.
Кути та окружність (середнє)