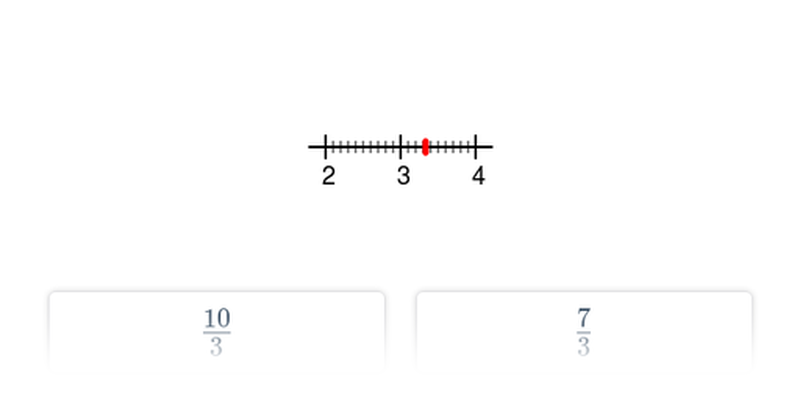
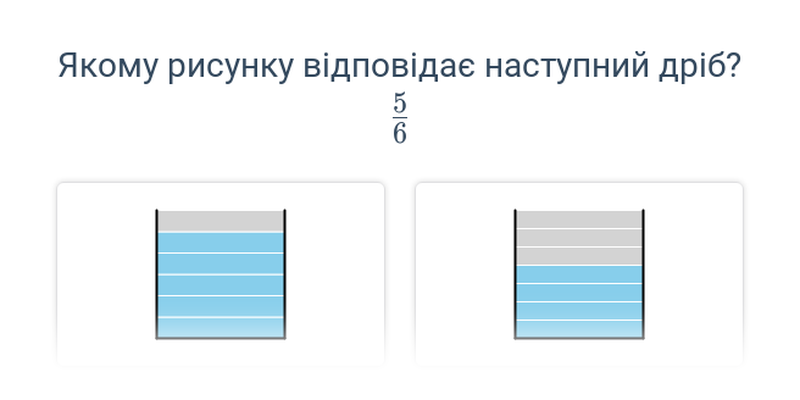
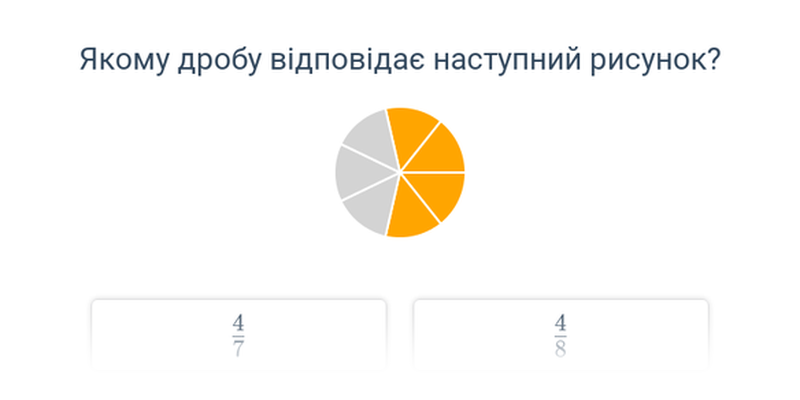
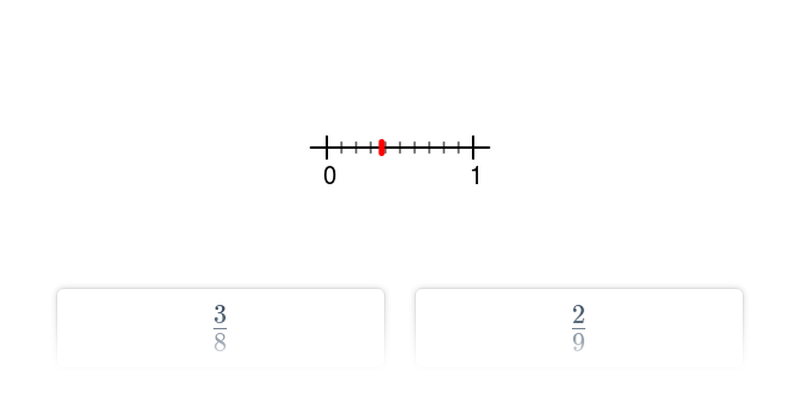
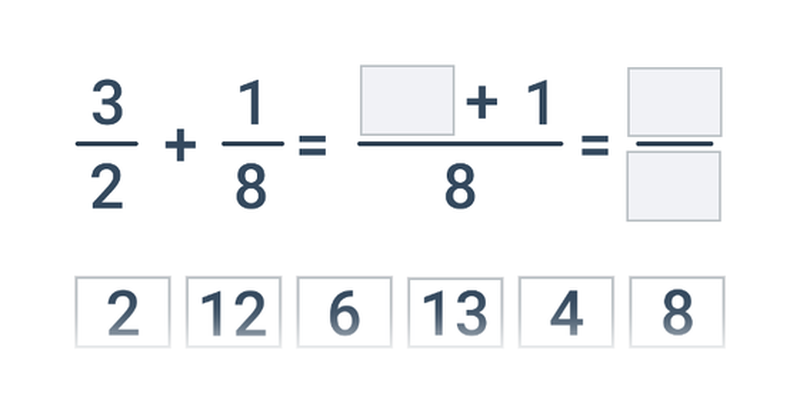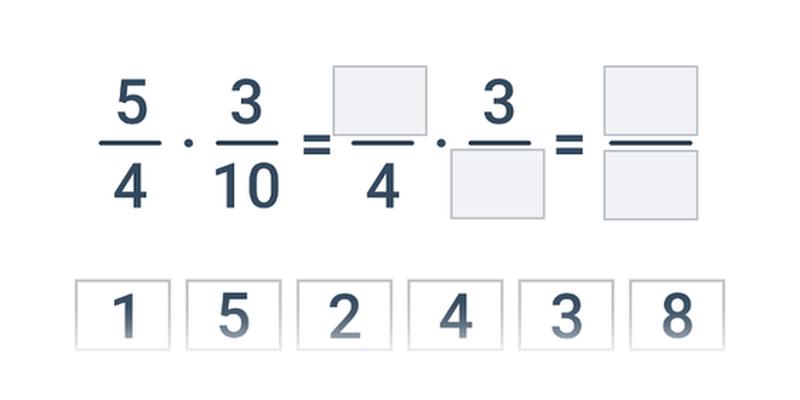Дроби

Дроби записуємо у вигляді \frac{a}{b}, де a називається чисельником, а b — знаменником. Щоб дріб мав сенс, знаменник не має дорівнювати нулю. Значення дробу відповідає діленню. Приклад: у дробі \frac32 чисельником є число 3, а знаменником — число 2, значення дробу \frac32 дорівнює діленню 3:2 = 1{,}5.

Розширення і скорочення

Значення дробу не змінюється при розширенні і скороченні (ненульовим числом c).

Розширення числом c:	\frac{a}{b} = \frac{c\cdot a}{c \cdot b}
Скорочення числом c:	\frac{a}{b} = \frac{a:c}{b:c}

Приклади:

Розширення дробу \frac64 числом 5: \frac64 = \frac{6\cdot 5}{4\cdot 5} = \frac{30}{20}.
Скорочення дробу \frac64 числом 2: \frac64 = \frac{6:2}{4:2} = \frac{3}{2}.

Звичайна форма

Завдяки розширенню та скороченню ми можемо одну й ту саму величину записати нескінченною кількістю різних дробів. Дріб \frac{a}{b} знаходиться у звичайній формі, якщо числа a, b мають єдиний спільний дільник — число 1.

Приклади:

Дріб \frac64 не є у звичайній формі, тому що числа 6 і 4 мають спільний дільник 2. Отже, дріб можна ще скоротити.
Дріб \frac34 є у звичайній формі, тому що числа 3 та 4 мають одиницю як єдиний спільний дільник.

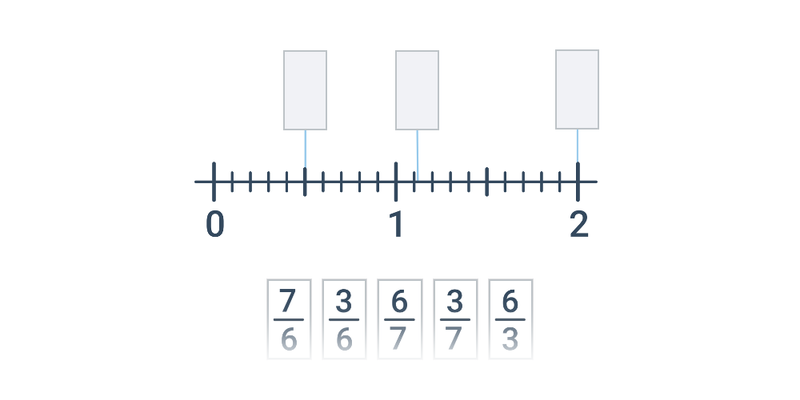
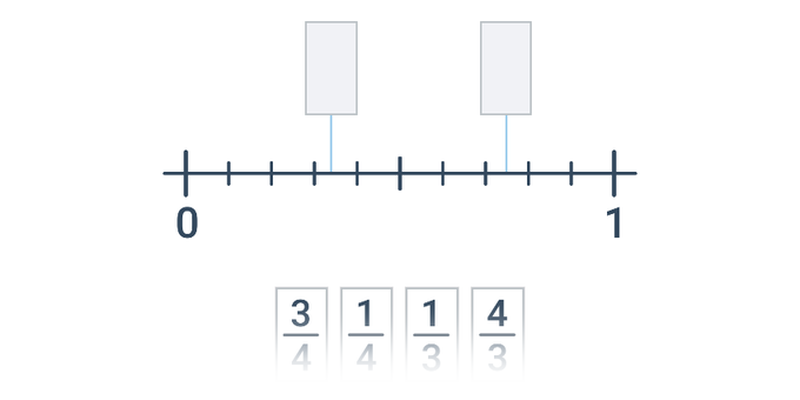
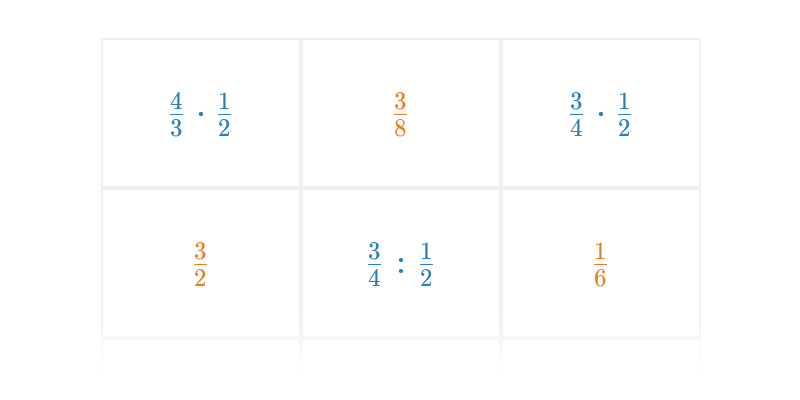
Переміщення

Переміщення карт на правильне місце. Просте управління, цікаві та оригінальні завдання.

Дроби

Дроби: основні поняття

Ознайомлення з дробами

Дроби на числовій прямій

Порівняння дробів

Обчислення з дробами

Скорочення дробів

Додавання та віднімання дробів

Множення і ділення дробів

Скорочення дробів

Переміщення • середній

Скорочення дробів

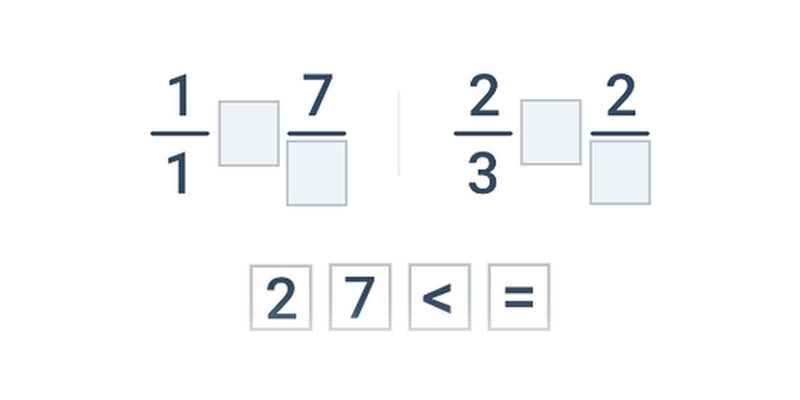
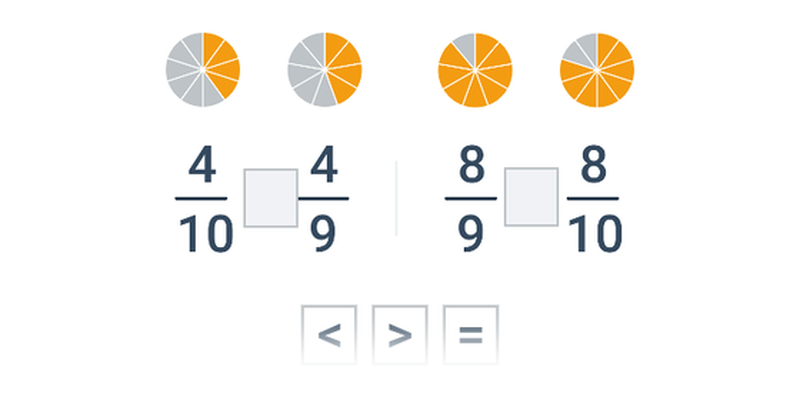
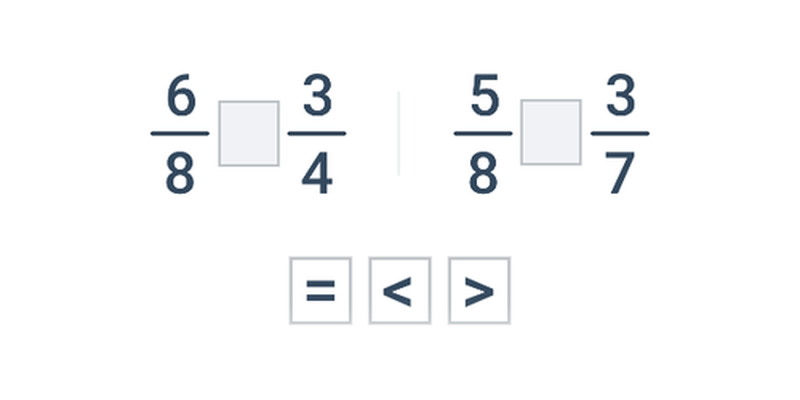
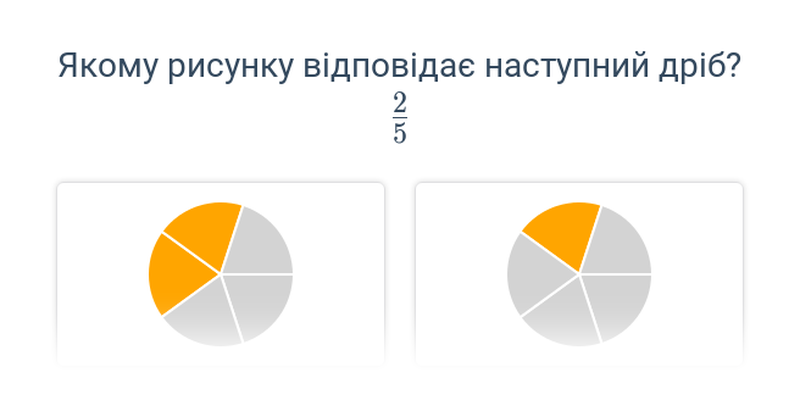
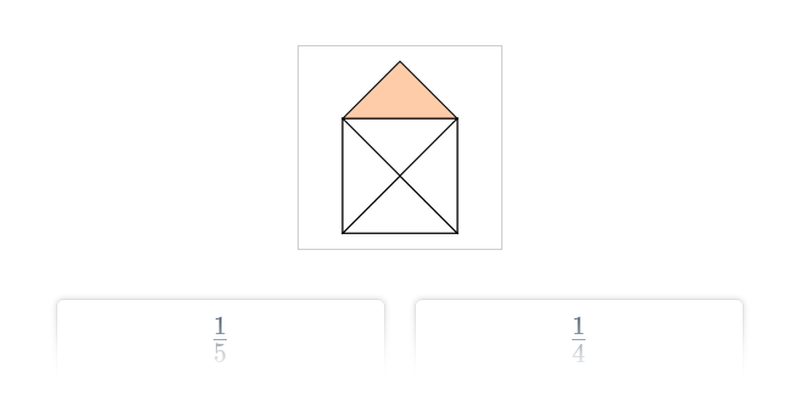
Вибір

Швидке практикування шляхом вибору з двох варіантів.

Дроби

Дроби: основні поняття

Ознайомлення з дробами

Дроби на числовій прямій

Порівняння дробів

Мішані числа

Дроби: основи, мікс

Обчислення з дробами

Скорочення дробів

Додавання та віднімання дробів

Множення і ділення дробів

Розрахунки з дробами: мікс

Просунута лічба з дробами

Дроби, степені, корені

Порівняння дробів

Вибір • складне

Порівняння дробів

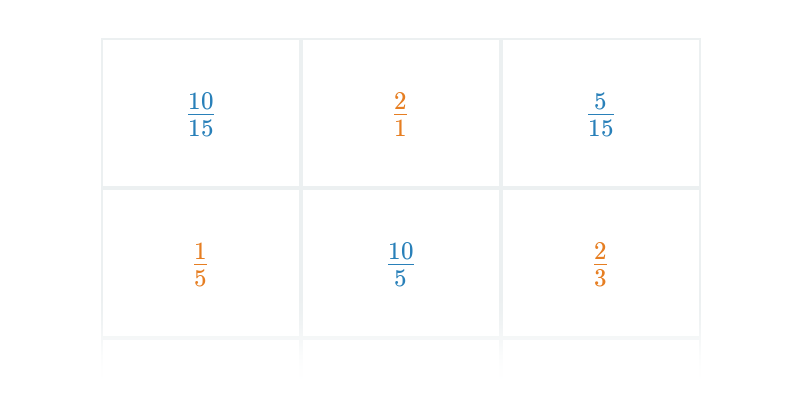
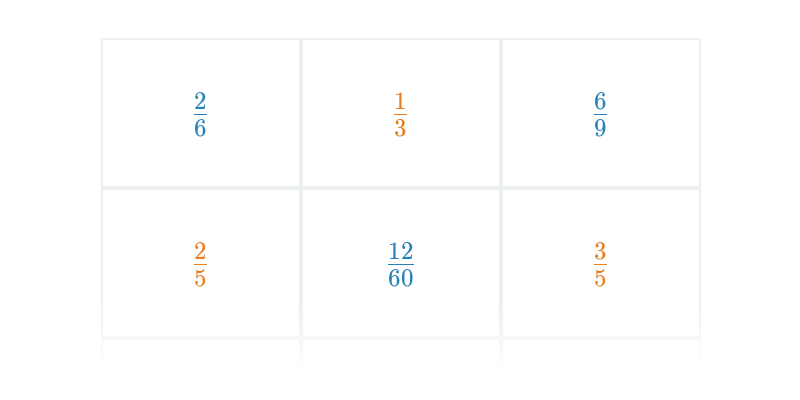
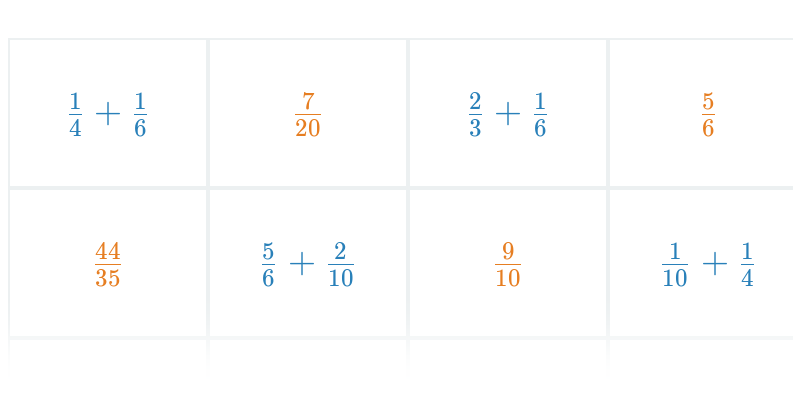
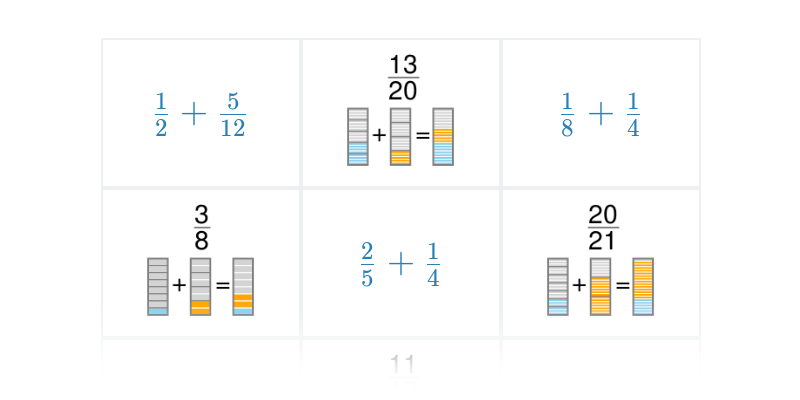
Pexeso

Вправа на знаходження пар.

Дроби

Дроби: основні поняття

Ознайомлення з дробами

Дроби словами

Дроби на числовій прямій

Мішані числа

Обчислення з дробами

Скорочення дробів

Додавання та віднімання дробів

Дроби: додавання за допомогою картинок

Множення і ділення дробів

Додавання та віднімання дробів

Pexeso • середній

Додавання та віднімання дробів

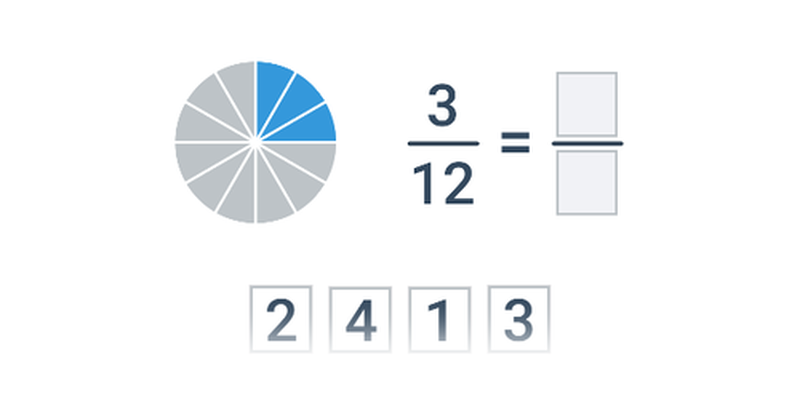
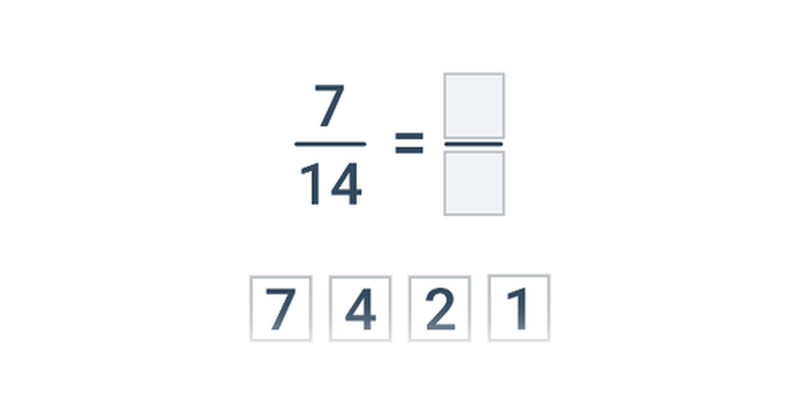
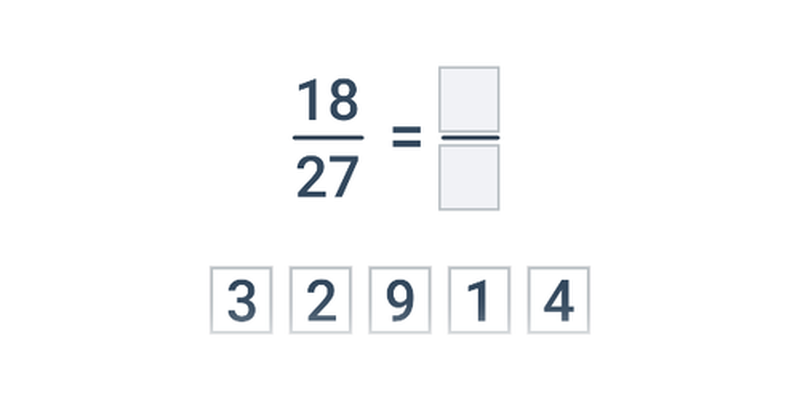
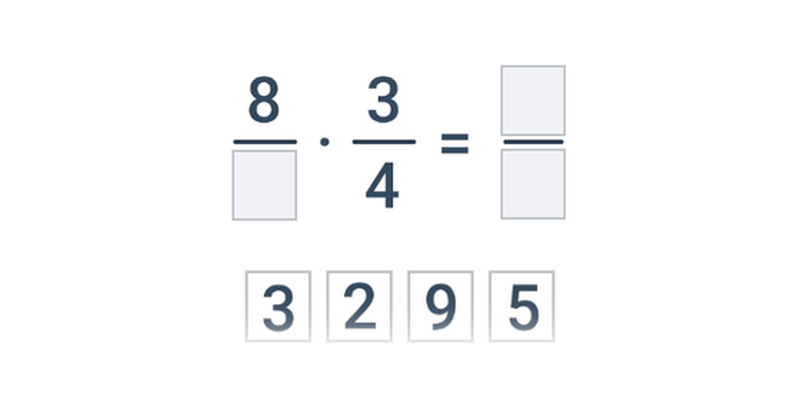
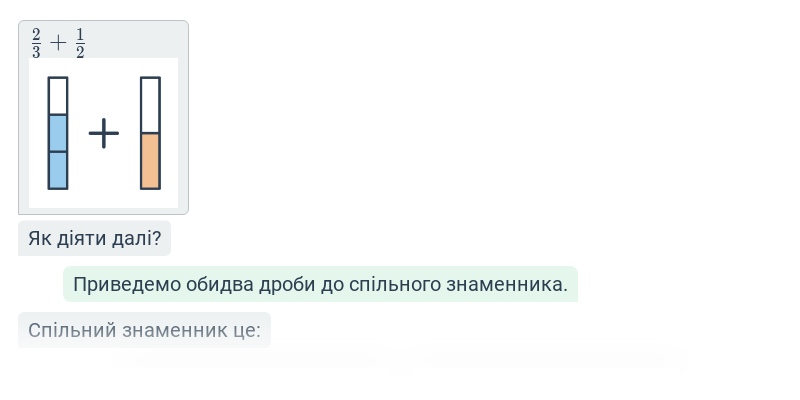
Крок за кроком

Доповнення окремих кроків в рамках комплексної роботи.

Дроби

Обчислення з дробами

Скорочення дробів

Додавання та віднімання дробів

Додавання і віднімання дробів за допомогою картинок

Множення і ділення дробів

Скорочення дробів

Крок за кроком • середній

Скорочення дробів

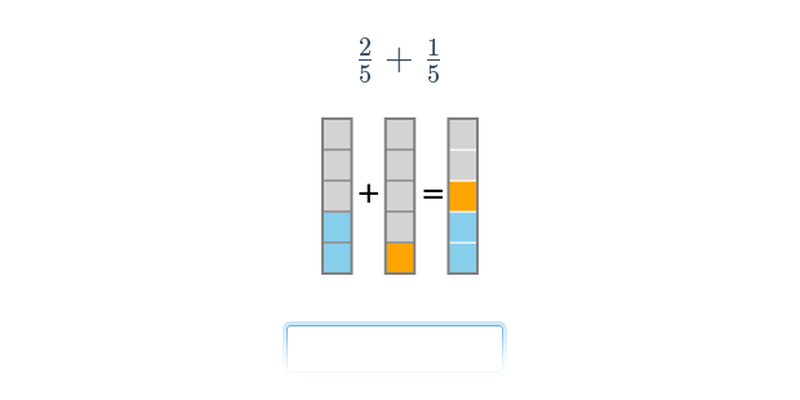
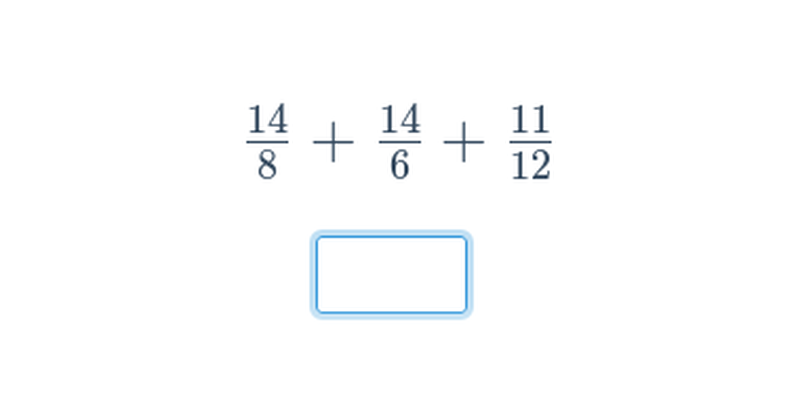
Письмова відповідь

Вправа, в якій ви набираєте відповідь на клавіатурі.

Дроби

Дроби: основні поняття

Ознайомлення з дробами

Дроби на числовій прямій

Мішані числа

Обчислення з дробами

Скорочення дробів

Додавання та віднімання дробів

Додавання дробів з малюнками

Додавання дробів, де відповідь є цілим числом

Множення і ділення дробів

Поєднання операцій з дробами

Розрахунки з дробами: мікс

Ознайомлення з дробами

Письмова відповідь • легке

Ознайомлення з дробами

Словесні завдання

Класичне практикування словесних вправ, з різноманітними завданнями та пояснювальними текстами.

Дроби

Обчислення з дробами

Розрахунки з дробами: мікс

Розрахунки з дробами: мікс

Словесні завдання • середній

Розрахунки з дробами: мікс

Роботи

Перегони на швидкість проти роботів. Просте управління шляхом вибору з двох варіантів.

Дроби

Дроби: основні поняття

Ознайомлення з дробами

Порівняння дробів

ЗВ’ЯЖІТЬСЯ З НАМИ

Дякуємо за ваше повідомлення, його було успішно відправлено.

Напишіть нам

Вам потрібна допомога?

Будь ласка, спочатку ознайомтеся з поширеними запитаннями:

Поширені запитання

Про що йдеться у повідомленні?

Повідомлення Зміст Управління Вхід до системи Ліцензія