Арифметична і геометрична послідовність
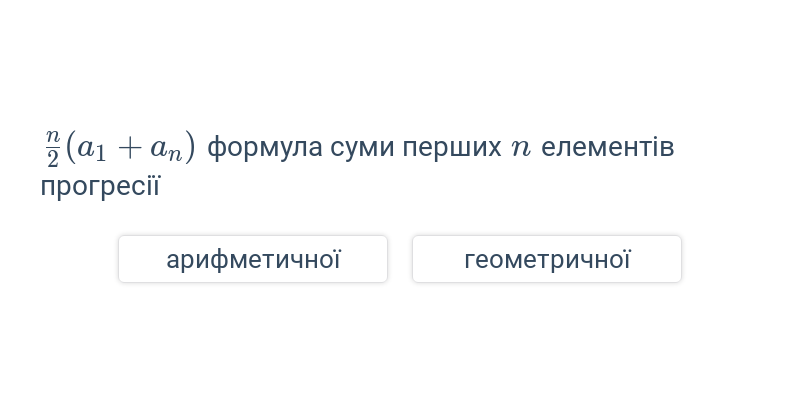
Арифметична послідовність – це математична послідовність, в якій між кожними двома послідовними членами є постійна різниця. Ця різниця зазвичай позначається як d і називається диференцією.
- Рекурентне співвідношення: a_n = a_{n-1} + d
- Формула для n-го члена: a_n = a_1+ (n-1)\cdot d
- Приклади:
- 1, 3, 5, 7, 9, 11, ... (a_1=1, d=2)
- 20, 17, 14, 11, 8, ... (a_1=20, d=-3)
- 300, 305, 310, 315, 320, ... (a_1=300, d=5)
Геометрична послідовність – це математична послідовність, в якій між кожними двома послідовними членами є постійне відношення. Це відношення зазвичай позначається як q.
- Рекурентне співвідношення: a_n = q \cdot a_{n-1}
- Формула для n-го члена: a_n = q^{n-1}\cdot a_1
- Приклади:
- 1, 2, 4, 8, 16, 32, ... (a_1=1, q=2)
- 1000, 100, 10, 1, 0{,}1, 0{,}01, ... (a_1=1000, q=0,1)
- 5, 15, 45, 135, 405, ... (a_1=5, q=3)
- 8, -8, 8, -8, 8, -8, ... (a_1=8, q=-1)
Вибір
Швидке практикування шляхом вибору з двох варіантів.