Осьова симетрія визначається прямою o і приписує кожній точці X поза віссю таку точку X', що пряма o є віссю відрізка XX'. Іншими словами: відображення має однакову відстань від осі, як і початкова точка, і відрізок, що з’єднує точки, перпендикулярний до осі. Осьова симетрія зберігає відстані та кути, тому є видом конгруенції.

Приклади

Сині та помаранчеві фігури є взаємно осесиметричними відносно осі o:

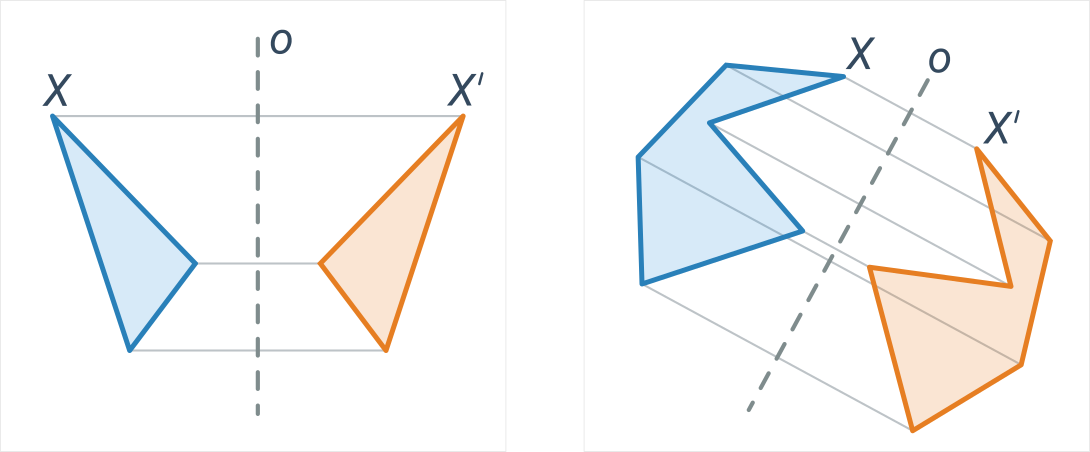
Для кращого розуміння може бути корисно порівняти осьову симетрію та центральну симетрію.

Осесиметрична фігура

Фігуру називаємо осесиметричною, якщо в деякій осьовій симетрії вона є відображенням самої себе. Вісь цієї симетрії називаємо віссю фігури. На рисунку наведено приклади осесиметричних фігур (зелені, з позначеними осями симетрії) і несиметричних (червоні):

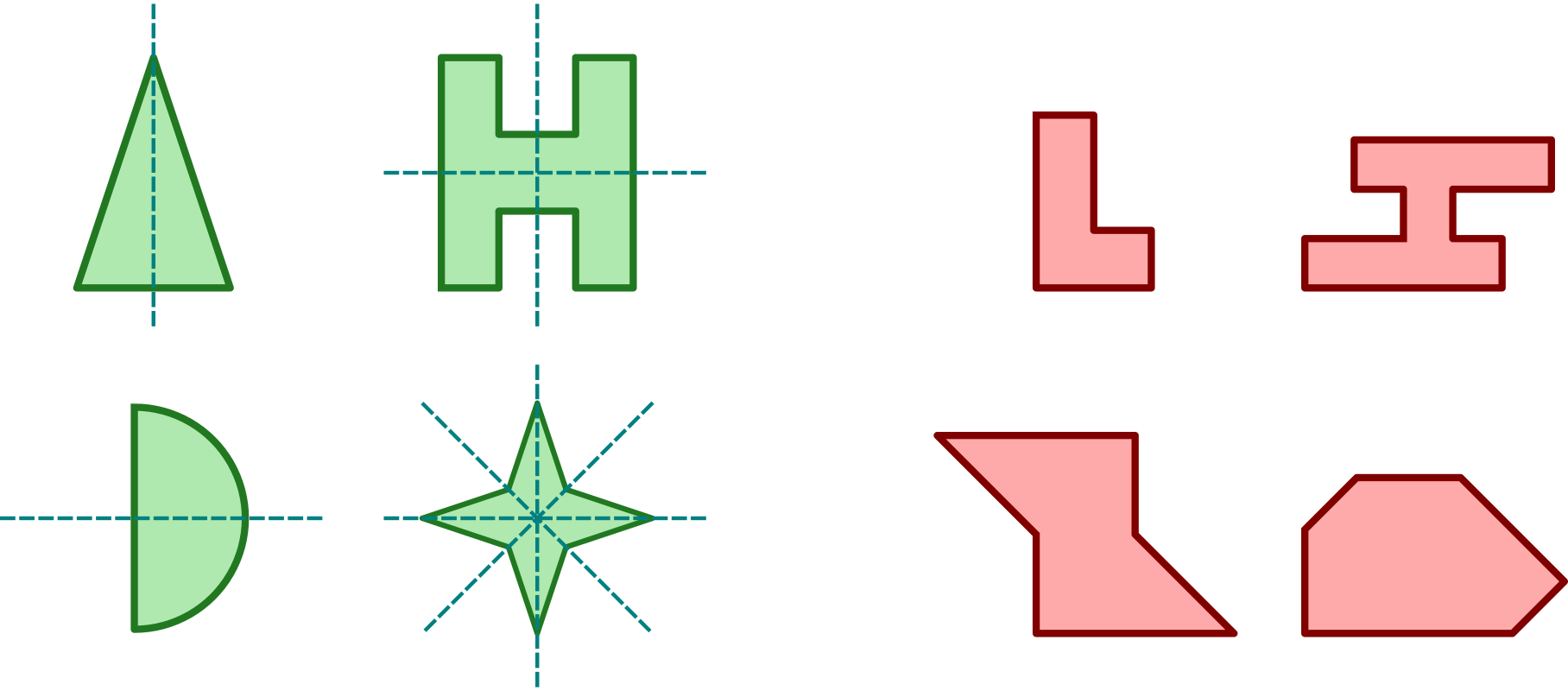
Інші приклади:

• Відрізок є осесиметричним і має у площині єдину вісь симетрії (перпендикуляр у його центрі).
• Рівнобедрений трикутник є осесиметричним.
• Трикутник, який не є рівнобедреним, не є осесиметричним.
• Усі правильні багатокутники є осесиметричними. Кількість осей симетрії дорівнює кількості вершин багатокутника.
• Коло є осесиметричним і має нескінченно багато осей симетрії.