Периметр трикутника
Периметр трикутника обчислюється, як сума довжин його сторін: o=a+b+c
Приклад:
Трикутник на малюнку має довжини сторін a=10, b=8, c=14, отже його периметр дорівнює o=a+b+c=10+8+14=32.
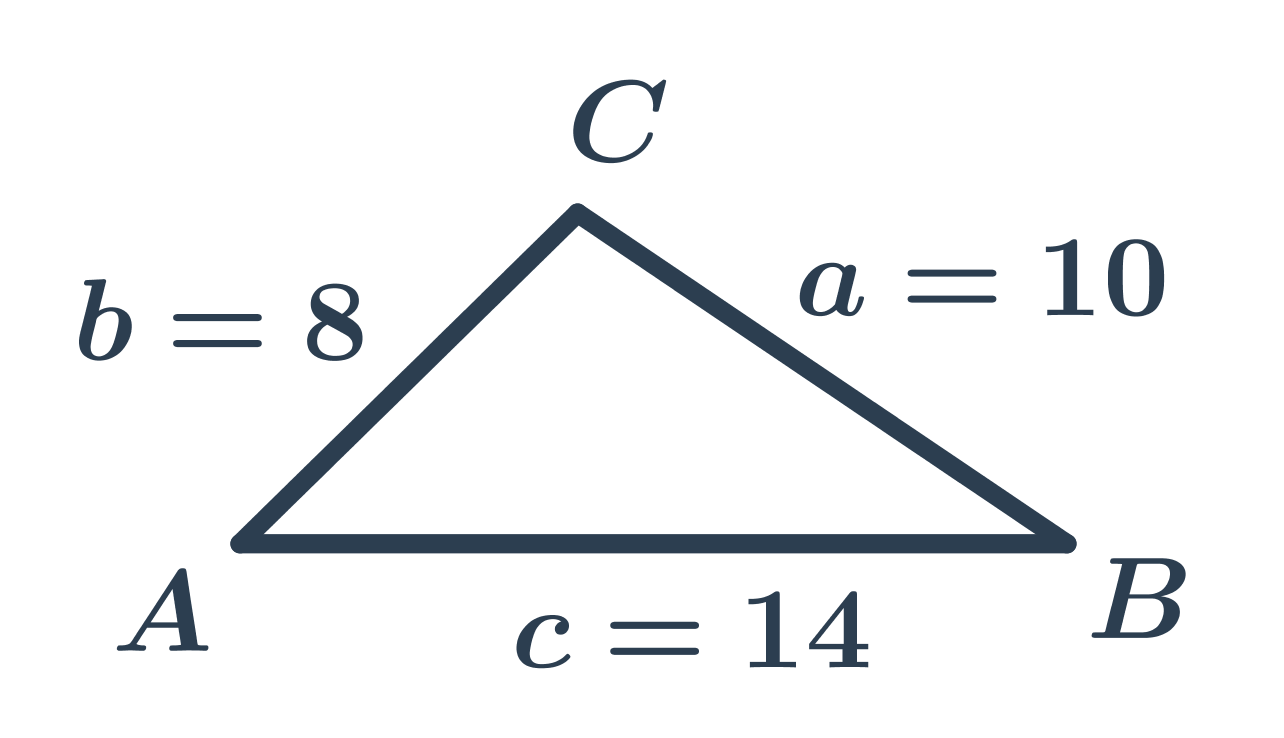
Периметр квадрата і прямокутника
Периметр квадрата зі стороною, довжина якої a, обчислюється як o=a+ a+a+a= 4a.
Периметр прямокутника зі сторонами, довжини яких a,b, дорівнює o=a + b + a + b = 2\cdot (a+b).
ВгоруПериметр паралелограма
Периметр ромба зі сторонами довжини a,b обчислюється, як S=a + b + a + b = 2\cdot (a+b).
ВгоруПериметр трапеції
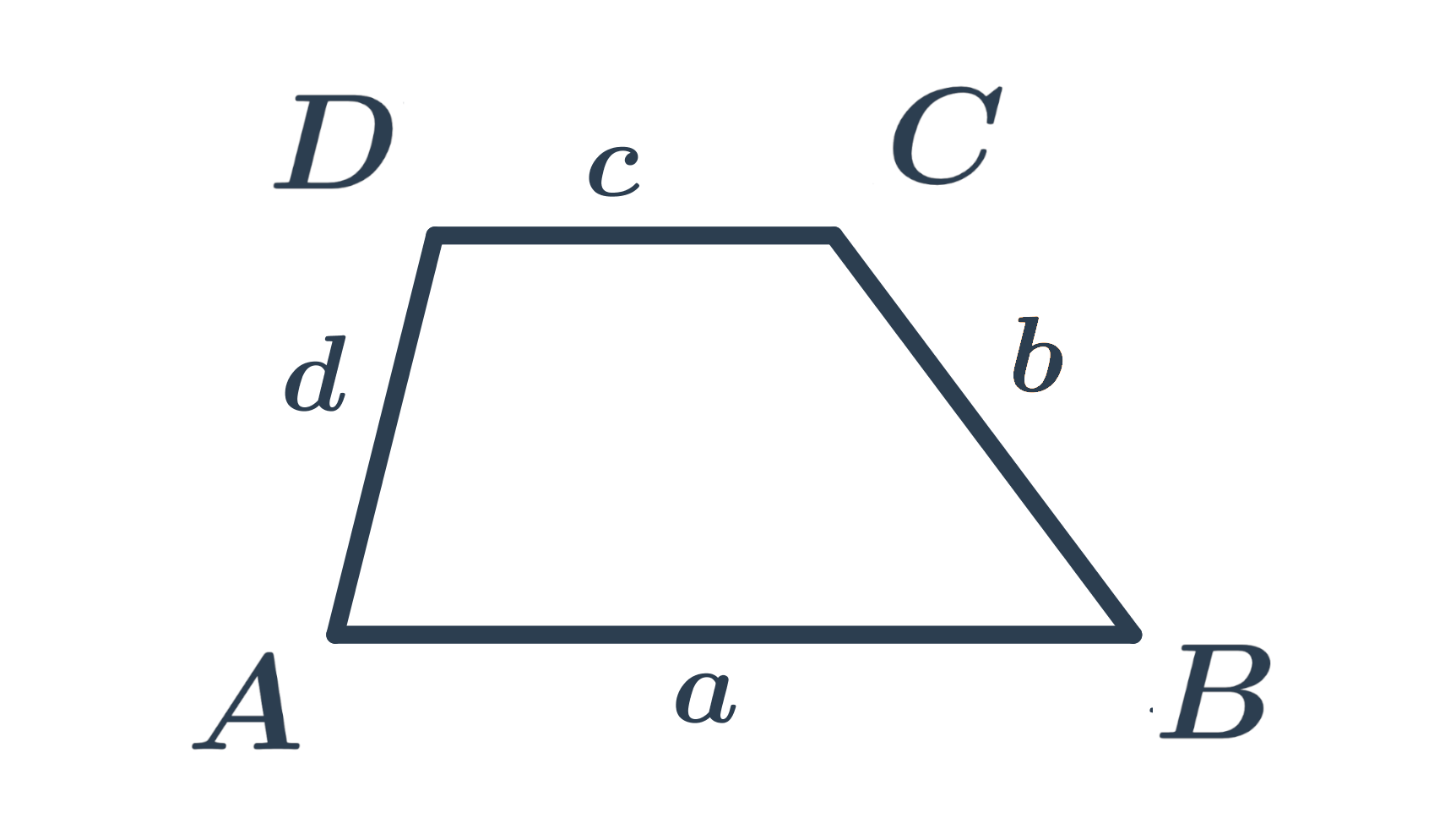
Периметр трапеції обчислюється, як сума довжин її сторін. Таким чином, периметр трапеції ABCD зі сторонами довжини a,b,c,d обчислюється за формулою o=a+b+c+d.
Довжина круга, довжина окружності
Формула для периметра кола
Периметра кола (або круга) з радіусом r обчислюється за формулою o=2\pi r. Для діаметра d є дійсним o = \pi d.
Константа \pi також відома як число Людольфа. \pi є ірраціональним числом, що означає, що його неможливо виразити у вигляді простого дробу або записати точно в десятковій системі. Приблизне значення \pi становить 3,141 592 65.
При обчисленні периметра кола важливо уникати плутанини між радіусом і діаметром, що часто спричиняє помилки.
Інтуїція
Інтуїцію в контексті периметра кола можна розглянути на рисунку нижче. Периметр оранжевого квадрата дорівнює 8\cdot r. Периметр кола є “трохи меншим” – приблизно 2\pi \cdot r \approx 6{,}3 \cdot r.

Приклади
- Нехай коло має радіус 3 см. Його периметр становить 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm.
- Круг з діаметром 2 см має довжину \pi \cdot 2 \approx 6,3 см.
- Центральне коло на футбольному полі має радіус 9{,}1 метра. Щоб обійти його по зовнішньому краю, потрібно пройти 2 \pi \cdot 9{,}1 \approx 57 метрів.
Довжина дуги кола
Довжина дуги
Довжину дуги, яка на колі з радіусом r відповідає центральному куту \alpha, обчислюємо за формулою: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Приклади
- Довжина дуги на рисунку дорівнює: \frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
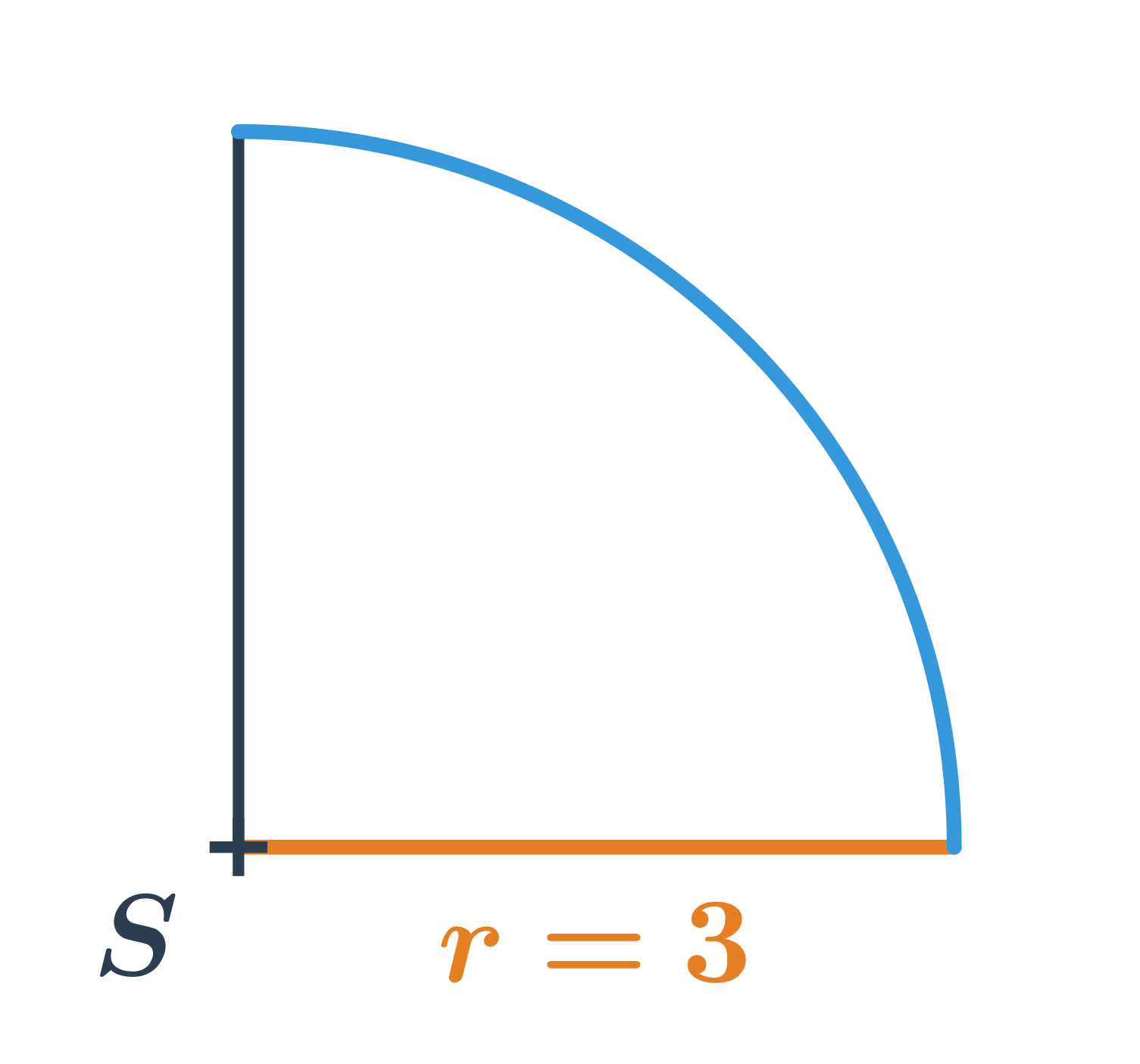
- Довжина всього кола (тобто для повного кута 360^{\circ}) дорівнює: \frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Периметр: мікс
Периметр у трикутників і чотирикутників — це просто сума довжин їхніх сторін.
| Фігура | Властивості | Периметр |
|---|---|---|
| трикутник | сторони a, b, c | o = a + b + c |
| квадрат | сторона a | o = 4a |
| прямокутник | сторони a, b | o = 2(a+b) |
| паралелограм | сторони a, b | o = 2(a+b) |
| довільний чотирикутник | сторони a, b, c, d | o = a+b+c+d |
Площа квадрата і прямокутника
Площа квадрата зі стороною довжиною a дорівнює S=a\cdot a=a^2.
Площа прямокутника зі сторонами довжинами a,b дорівнює S=a\cdot b.
ВгоруПлоща круга
Формула для обчислення площі кола
Площа кола з радіусом r дорівнює S=\pi r^2. Для діаметра d маємо S = \frac{1}{4} \pi d^2.
Константа \pi також називається числом Людвіга. \pi є ірраціональним числом, що означає, що його неможливо виразити дробом або точно записати в десятковій системі. Приблизне значення \pi дорівнює 3,141 592 65.
Під час обчислення площі кола слід бути уважним, чи використовуємо ми радіус, чи діаметр. Плутанина між діаметром і радіусом є частою помилкою.
Інтуїція
Основні навички інтуїції для обчислення площі кола ілюструє наведений нижче малюнок. Жовті квадрати мають площу r^2. Помаранчевий квадрат складається з чотирьох жовтих квадратів, тому його площа 4\cdot r^2. Коло має “трохи меншу” площу, ніж помаранчевий квадрат, що відповідає тому, що площа кола приблизно дорівнює 3{,}14 \cdot r^2.

Приклади
- Нехай маємо коло з радіусом 3 см. Його площа дорівнює \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 см².
- Розглянемо коло з діаметром 2 см. Його внутрішня область має площу \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 см².
- Центральне коло на футбольному полі має радіус 9{,}1 метра. Якщо б ми хотіли пофарбувати всю траву в колі в рожевий колір, нам би потрібно було пофарбувати \pi \cdot 9{,}1^2 \approx 260 м² трави.
Площа сектора круга
Площа сектора
Площу сектора з центральним кутом \alpha і радіусом r обчислюємо за формулою: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2
Приклади
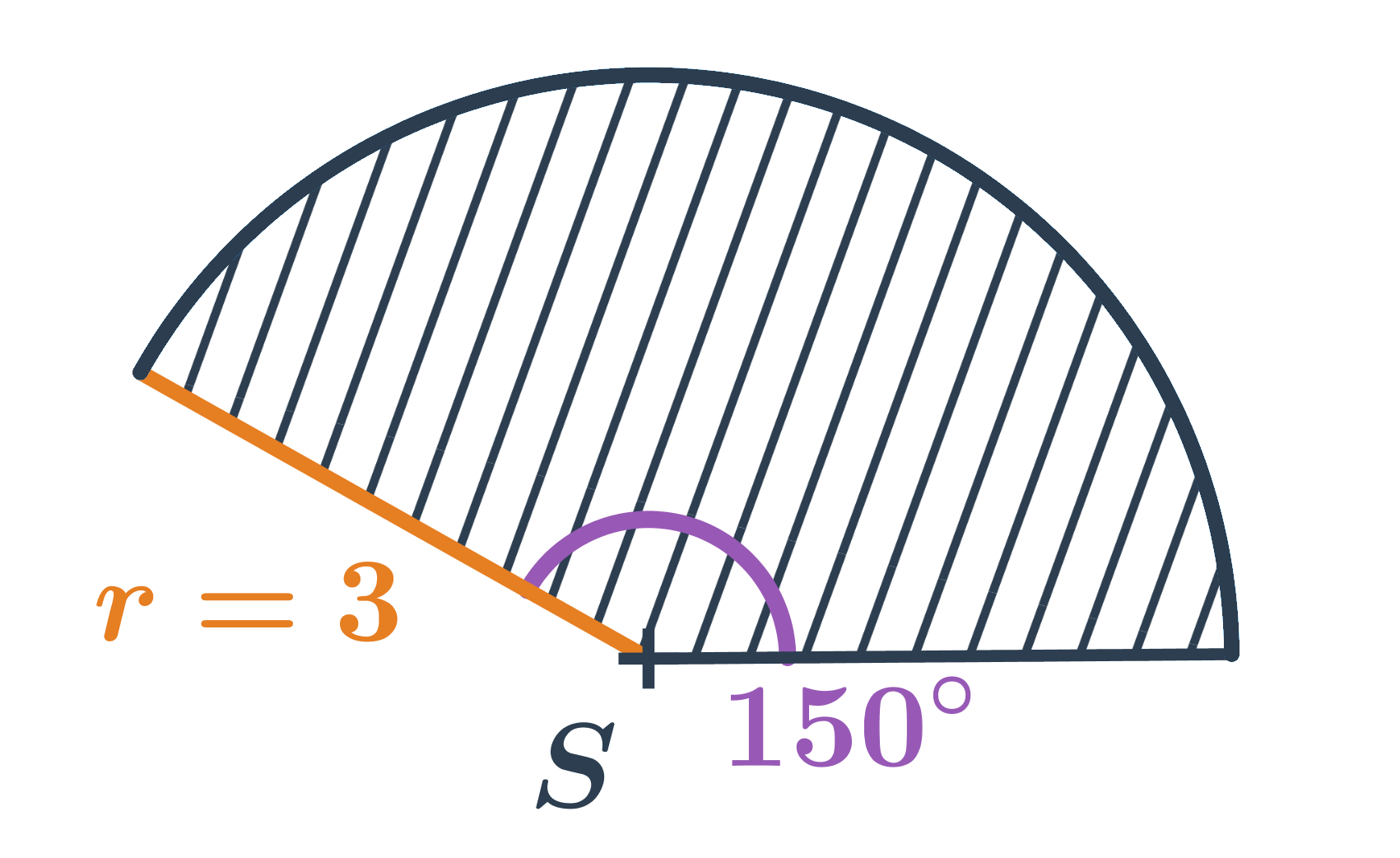
- Сектор на малюнку має площу: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi
- Площа цілого кола (сектора з центральним кутом 360^{\circ}) дорівнює: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2

