Дії та властивості на площині

Основні властивості геометричних трансформацій:

• Осьова симетрія: відображаємо “дзеркальне” зображення фігури відносно прямої.
• Центральна симетрія: відтворюємо фігуру відносно точки.
• Обертання: обертаємо фігуру навколо заданої точки на певний кут.
• Тотожність: дві фігури є тотожними, якщо вони мають однаковий розмір і форму (можуть відрізнятися поворотом та розташуванням).
• Подібність: дві фігури подібні, якщо вони мають однакову форму (можуть відрізнятися розміром, поворотом і розташуванням).

Тема визначення відображень у площині розглядає розрізнення між різними видами відображень.

Осьова симетрія визначається прямою o і приписує кожній точці X поза віссю таку точку X', що пряма o є віссю відрізка XX'. Іншими словами: відображення має однакову відстань від осі, як і початкова точка, і відрізок, що з’єднує точки, перпендикулярний до осі. Осьова симетрія зберігає відстані та кути, тому є видом конгруенції.

Приклади

Сині та помаранчеві фігури є взаємно осесиметричними відносно осі o:

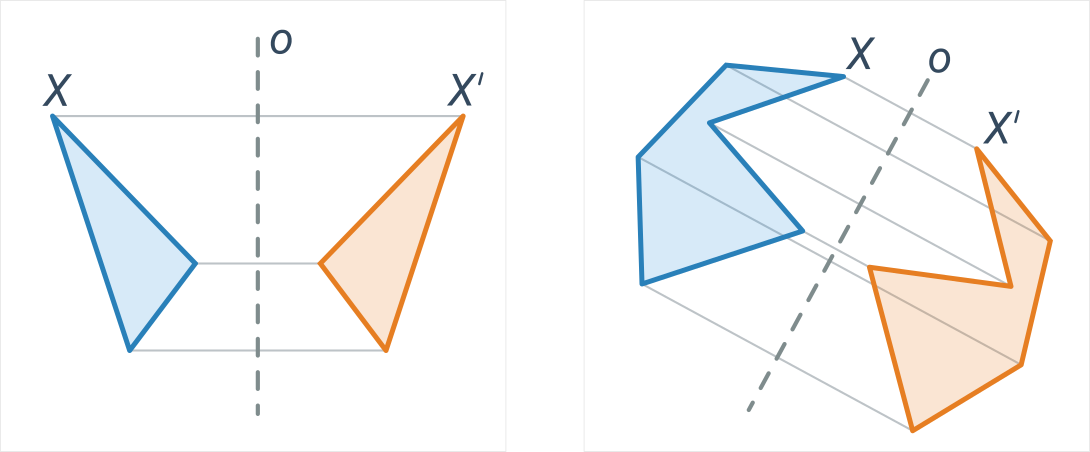
Для кращого розуміння може бути корисно порівняти осьову симетрію та центральну симетрію.

Осесиметрична фігура

Фігуру називаємо осесиметричною, якщо в деякій осьовій симетрії вона є відображенням самої себе. Вісь цієї симетрії називаємо віссю фігури. На рисунку наведено приклади осесиметричних фігур (зелені, з позначеними осями симетрії) і несиметричних (червоні):

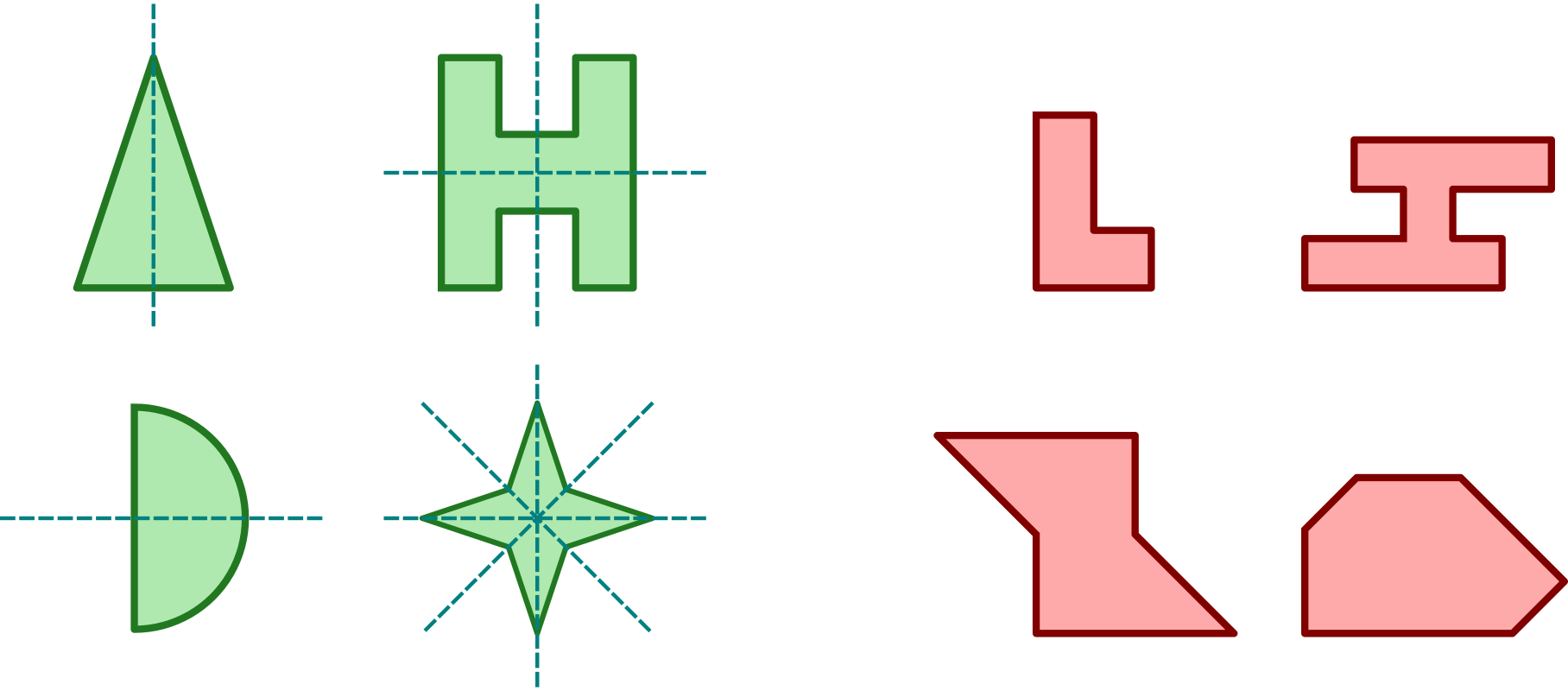
Інші приклади:

• Відрізок є осесиметричним і має у площині єдину вісь симетрії (перпендикуляр у його центрі).
• Рівнобедрений трикутник є осесиметричним.
• Трикутник, який не є рівнобедреним, не є осесиметричним.
• Усі правильні багатокутники є осесиметричними. Кількість осей симетрії дорівнює кількості вершин багатокутника.
• Коло є осесиметричним і має нескінченно багато осей симетрії.

Центральна симетрія визначається точкою S і приписує кожній точці X таку точку X', що точка S є центром відрізка XX'. Іншими словами, відображення має таку саму відстань від центра, як і початкова точка, і лежить на промені, протилежному до SX.

Центральна симетрія зберігає відстані та кути, отже, є видом конгруенції. Центральна симетрія з центром у точці S є тотожною обертанню на 180 градусів навколо центру S.

Приклади

Сині та оранжеві фігури є взаємно центрально симетричними відносно центра S:

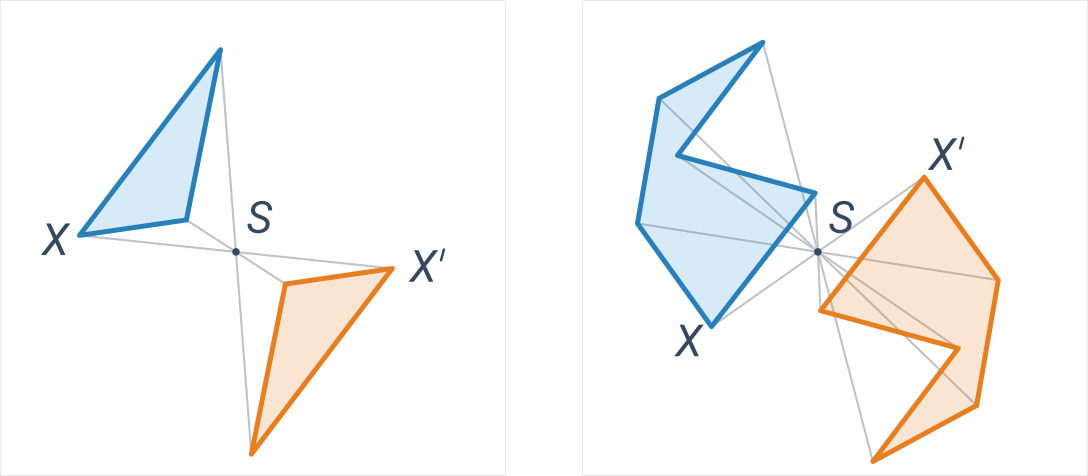
Для кращого розуміння може бути корисно порівняти центральну та осьову симетрію.

Центрально симетрична фігура

Фігуру називають центрально симетричною, якщо в деякій центральній симетрії вона є відображенням самої себе. Центр цієї симетрії називається центром симетрії об’єкта. На рисунку подано приклади центрально симетричних фігур (зелені, з позначеним центром симетрії) та несиметричних (червоні):

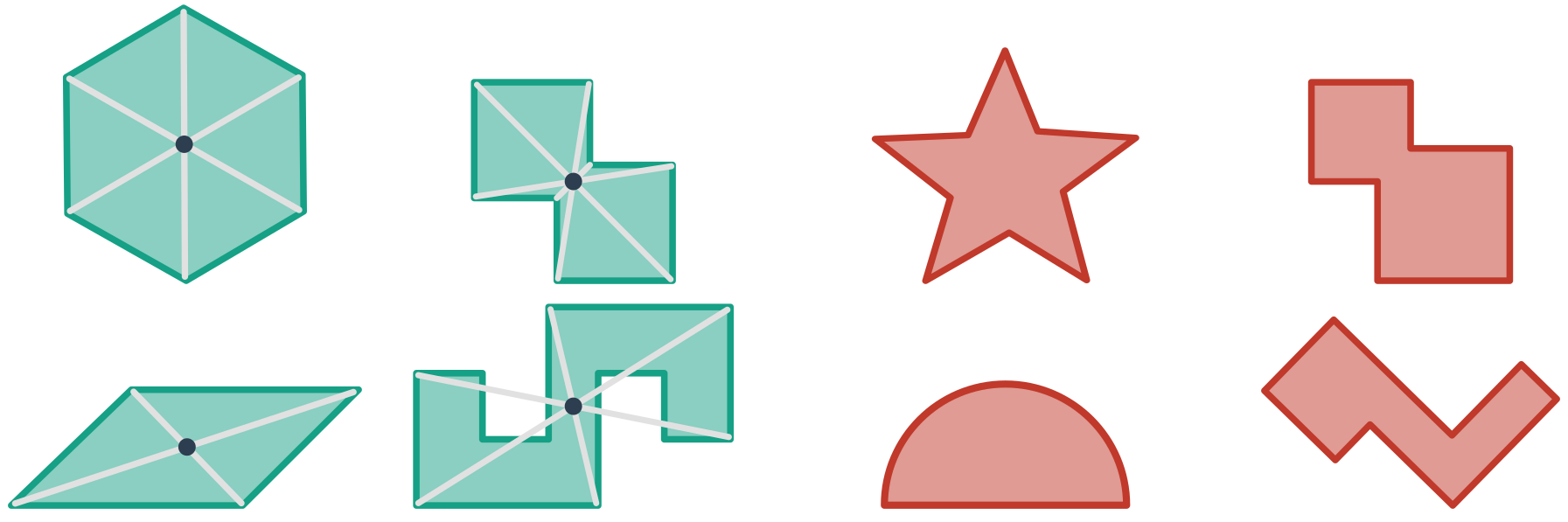
Інші приклади:

• Відрізок, прямокутник, квадрат, ромб, правильний шестикутник і коло є центрально симетричними.

• Жоден трикутник не є центрально симетричним.

Дві геометричні фігури є подібними, якщо вони мають однакову форму (незалежно від розміру). На рисунку нижче подібні фігури мають однаковий колір:

Точніше кажучи, фігури є подібними, якщо одну можна отримати з іншої за допомогою рівномірного зменшення або збільшення, а також зсуву, обертання або відображення.

Подібність зберігає величини кутів та співвідношення довжин.

Співвідношення довжин відповідних відрізків у обох фігурах називається коефіцієнт подібності.