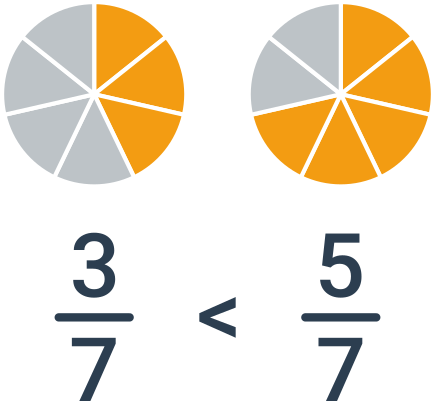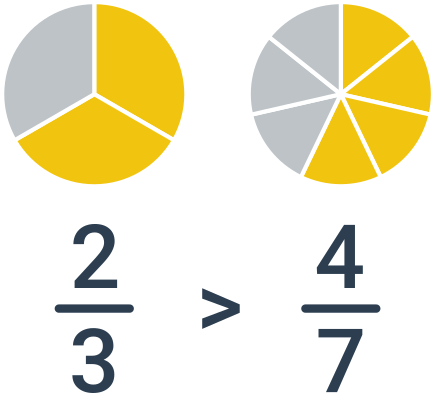Перш ніж розпочати порівняння дробів, важливо зрозуміти, що таке чисельник («те, що зверху») і знаменник («те, що знизу»). У дробі \frac{3}{7} 3 – це чисельник, а 7 – знаменник.

Порівняння дробів з однаковим знаменником

Порівнювати дроби з однаковим знаменником дуже просто: достатньо просто порівняти чисельники. Наприклад, якщо ми порівнюємо дроби \frac{3}{7} і \frac{5}{7}, більшим буде другий дріб. Обидва дроби виражають сьомі частини цілого, і п’ять сьомих більше, ніж три сьомих.

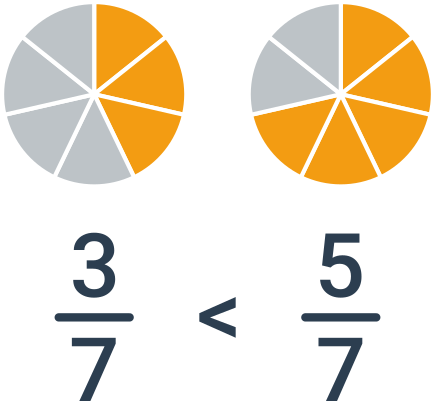
Порівняння дробів з однаковим чисельником

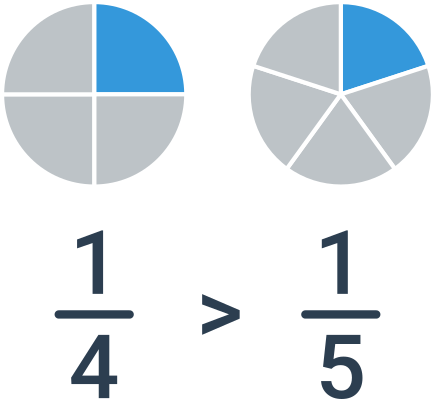
Якщо дроби мають однаковий чисельник, тоді потрібно порівняти знаменники. У цьому випадку порядок дробів буде протилежним до порядку знаменників. Якщо порівнюємо, наприклад, дроби \frac{1}{4} і \frac{1}{5}, більшим буде одна чверть: отримаю більший шматок піци, якщо її поділити на 4 частини, ніж якщо поділити на 5.

Різні знаменники і чисельники

У такому випадку нам потрібно спочатку звести дроби до спільного знаменника, а потім порівняти їх за чисельниками. Приклад: порівняння дробів \frac{2}{3} та \frac{4}{7}. Найменший спільний знаменник – 21, після розширення отримуємо пару дробів \frac{2}{3}=\frac{2\cdot 7}{3\cdot 7}=\frac{14}{21} та \frac{4}{7}=\frac{4\cdot 3}{7\cdot 3}=\frac{12}{21}. Оскільки 14 > 12, більшим є перший дріб, тобто \frac{2}{3}.

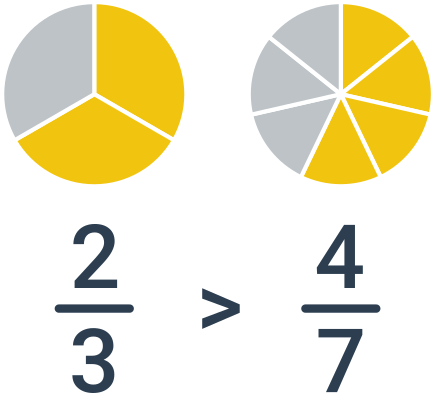
Порівняння без обчислень

Часто можна порівняти дроби без детальних обчислень, якщо правильно їх уявити або порівняти з відповідним значенням «посередині»:

• Дроби \frac{2}{3} і \frac{7}{6}. Перший з них менший за 1, другий більший за 1. Отже \frac{2}{3} < \frac{7}{6}.

• Дроби \frac{1}{3} і \frac{4}{5}. Перший з них явно менший за половину, другий значно більший за половину. Отже, \frac{1}{3} <\frac{4}{5}.