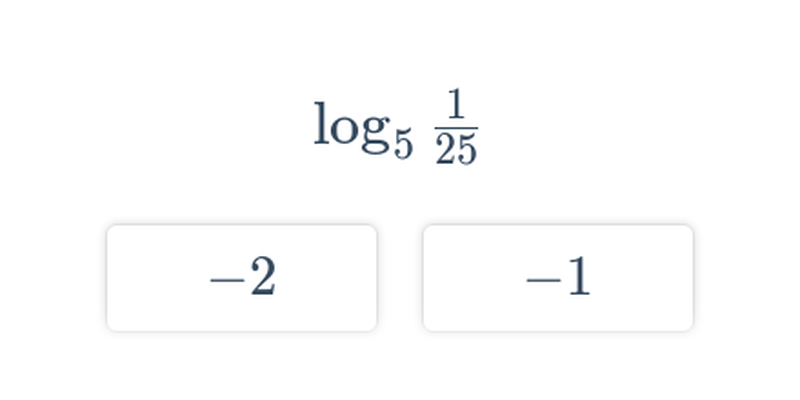Дякуємо за Ваш відгук.

Обчислення логарифмів

Логарифм додатного числа x з основою – це таке дійсне число y = \log_a(x), для якого виконується a^y = x. Приклади:

\log_{10}(100) = 2	, тому що 10^2 = 100
\log_2(32) = 5	, тому що 2^5 = 32
\log_5(125) = 3	, тому що 5^3 = 125
\log_7(1) = 0	, тому що 7^0 = 1
\log_2(0{,}5) = -1	, тому що 2^{-1} = \frac{1}{2} = 0{,}5

Вибір

Швидке практикування шляхом вибору з двох варіантів.

Обчислення логарифмів

Вибір • складне

Pexeso

Вправа на знаходження пар.

Обчислення логарифмів

Pexeso • складне

Письмова відповідь

Вправа, в якій ви набираєте відповідь на клавіатурі.

Обчислення логарифмів

Письмова відповідь • складне

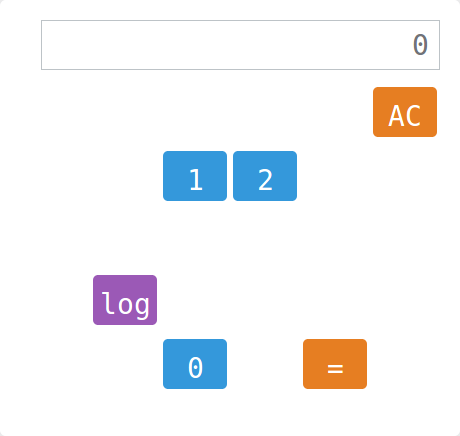
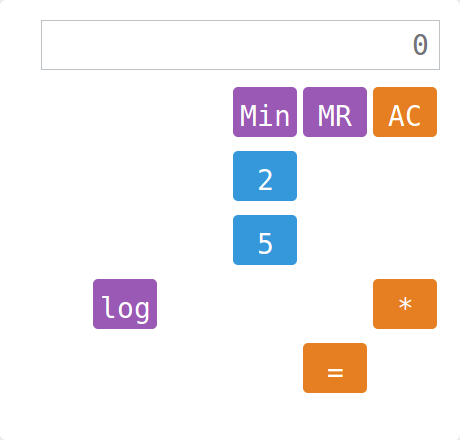
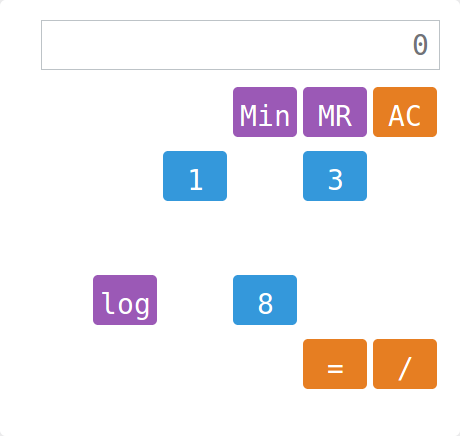
Калькулятор

Потрібно вивести на екран калькулятора вказані числа. Проблема полягає у тому, що на ньому відсутні деякі кнопки...

Логарифм

Зламаний калькулятор

Попередній

Подальший

Вправи

Обчислення логарифмів

Вибір