Дроби та десяткові числа – 5 клас

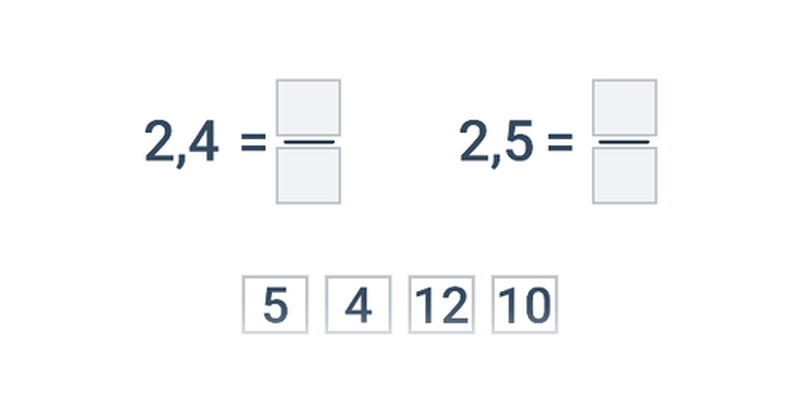
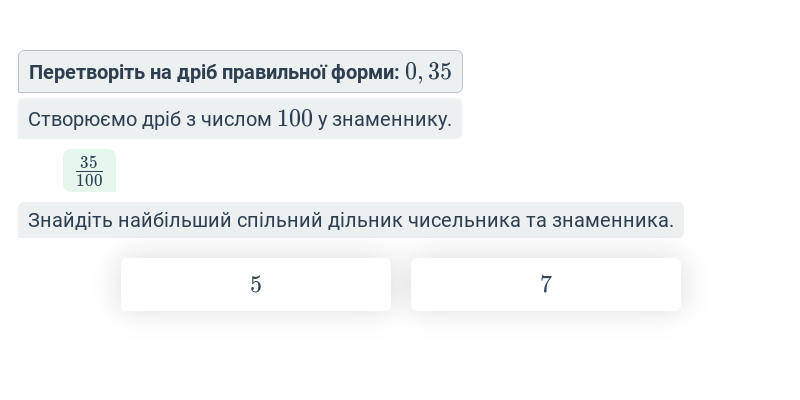
Перетворення десяткового числа на звичайний дріб

Десяткове число множимо на число, кратне десяти так, щоб «позбутися» десяткової коми. Потім скорочуємо дріб (найбільшим спільним дільником), щоб отримати дріб у найпростішому вигляді. Приклади:

• 1{,}5 = 1{,}5\cdot \frac{10}{10} = \frac{1{,}5\cdot 10}{10} = \frac{15}{10} = \frac{3}{2}

• 1{,}25 = 1{,}25 \cdot \frac{100}{100} = \frac{1{,}25\cdot 100}{100} = \frac{125}{100} = \frac{5}{4}

Розрахунки можуть бути простішими, якщо запам’ятати деякі корисні перетворення, за допомогою яких можна вирішити й інші приклади:

• 0{,}01 = \frac{1}{100}

• 0{,}1 = \frac{1}{10}

• 0{,}2 = \frac{1}{5}

• 0{,}25 = \frac{1}{4}

• 0{,}333\ldots = \frac{1}{3}

• 0{,}5 = \frac{1}{2}

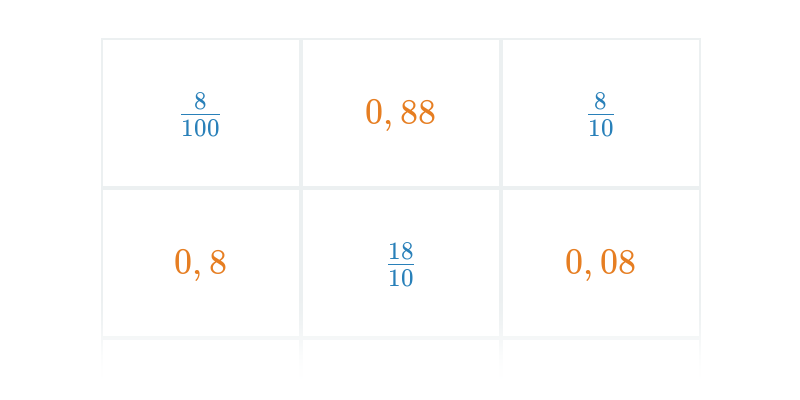
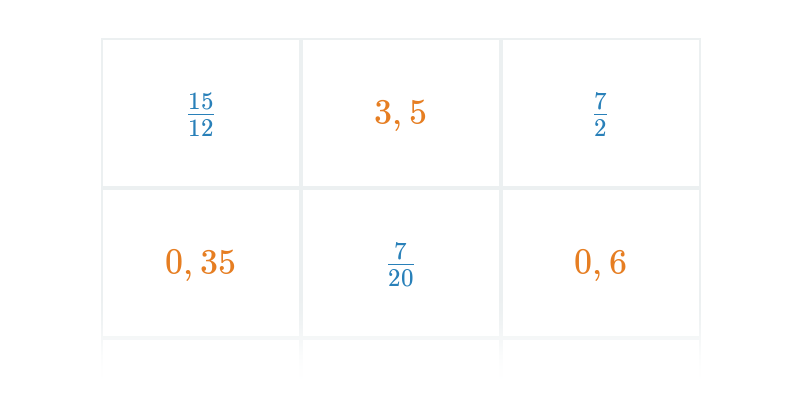
Перетворення звичайного дробу на десяткове число

Значення дробу – це просто частка чисельника і знаменника. Тому дріб можна виразити як десяткове число, просто поділивши чисельник на знаменник (може бути корисним використовувати метод «ділення стовпчиком»). Приклади:

• \frac{3}{4} = 3:4 = 0{,}75

• \frac{6}{5} = 6:5 = 1{,}2

• \frac{3}{20} = 3:20 = 0{,}15