Українська
Англійська
Інформатика
Znaiemo tse
Арифметика
Дроби, відсотки, десяткові числа
Геометрія
Елементарна алгебра
Функція
Одиниці вимірювання та час
Дискретна математика
Фінансова грамотність
Вибір
Pexeso
Крок за кроком
Письмова відповідь
Графікобудівник
Розуміння
Визначення
Переміщення
Решітка
Розділення
Зламаний калькулятор
Роботи
Стрілялка
Чудовиська
Перегони
Території
Командна гра
Мій обліковий запис
Вийти з системиПерелік коротких описів
Обчислення з дробами
Ви переглядаєтекороткі описи певних тем. Платформа Znaiemo tse зосереджується в основному на практичих вправах.. Ви можете отримати доступ до вправ з певної теми, перейшовши за посиланням нижче.
« Повернутися до практикування
Підрозділи
Додавання та віднімання дробів
Перш ніж почати додавати дроби, важливо розуміти, що таке чисельник («те, що зверху») і знаменник («те, що знизу»). У дробі \frac{3}{7} чисельник — це 3, а знаменник —7.
Додавання дробів із однаковим знаменником
Якщо дроби, які додаються, мають однаковий знаменник, достатньо просто додати чисельники. Знаменник залишаємо незмінним, тобто \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.
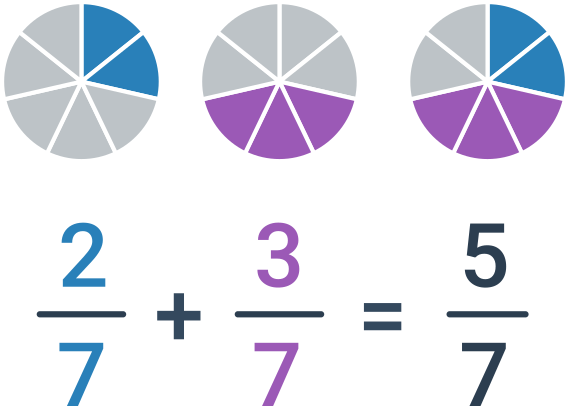
Додавання дробів з різними знаменниками
Якщо дроби мають різні знаменники, спочатку їх потрібно привести до спільного знаменника. Найзручніше привести дроби до найменшого спільного кратного початкових знаменників. Як тільки дроби мають однаковий знаменник, їх можна додавати за вказаним вище принципом.
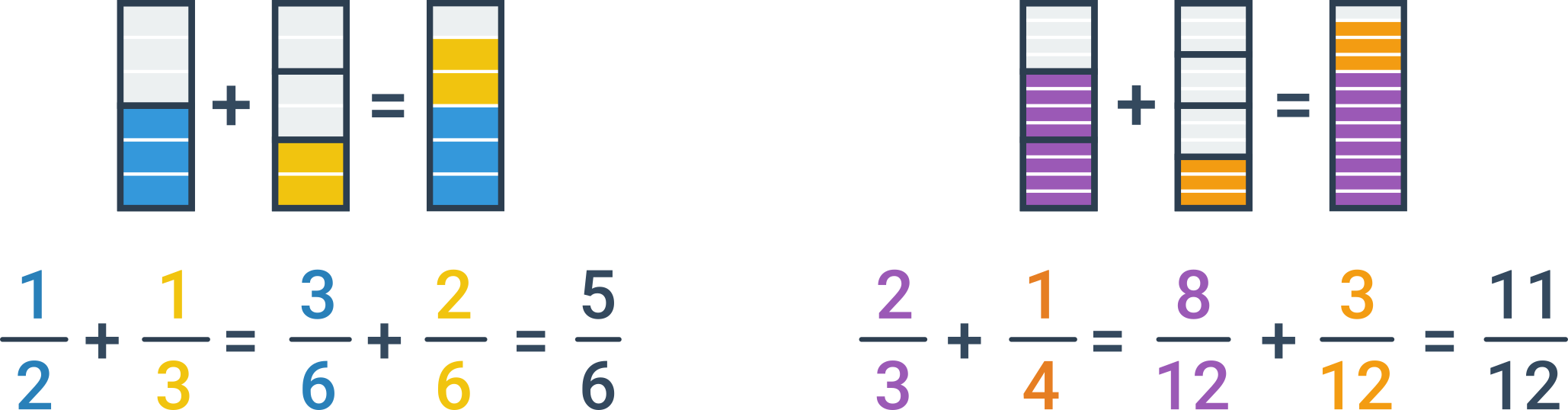
Скорочення та віднімання
Зазвичай отриманий дріб потрібно ще скоротити, щоб отримати результат у нескоротному вигляді. Віднімання дробів виконується так само, як і додавання.
Приклади
Приклади з однаковим знаменником без необхідності скорочення
\frac{2}{5} + \frac{1}{5} = \frac{2+1}{5} = \frac{3}{5}
\frac{5}{7} - \frac{2}{7} = \frac{5-2}{7} = \frac{3}{7}
Приклади з однаковим знаменником, де результат скорочується
\frac{5}{6}-\frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3}
\frac{8}{9} - \frac{2}{9} = \frac{8-2}{9} = \frac{6}{9} = \frac{2}{3}
Приклад із різними знаменниками: \frac{5}{6} - \frac{3}{4}
- Найменший спільний кратний знаменників 6 і 4 дорівнює 12, тому приводимо дроби до знаменника 12.
- \frac{5}{6} - \frac{3}{4} = \frac{5\cdot 2}{6\cdot 2} - \frac{3\cdot 3}{4\cdot 3}= \frac{10}{12} - \frac{9}{12} = \frac{1}{12}
Приклад із різними знаменниками: \frac{7}{8} + \frac{2}{5}
- Найменший спільний кратний знаменників 8 і 5 дорівнює 40, тому приводимо дроби до знаменника 40.
- \frac{7}{8} + \frac{2}{5} = \frac{7 \cdot 5}{8 \cdot 5} + \frac{2 \cdot 8}{5 \cdot 8} = \frac{35}{40} + \frac{16}{40} = \frac{51}{40}
Множення і ділення дробів
Множення дробів можна уявити за допомогою шоколаду. Якщо множимо \frac45\cdot \frac23, то це як взяти чотири з п’яти стовпчиків і два з трьох рядків. Скільки квадратів шоколаду ми візьмемо таким чином? Вісім з п’ятнадцяти, тобто \frac{8}{15}.
При множенні дробів ми просто множимо чисельники першого і другого дробів і отримуємо чисельник результату, аналогічно для знаменників: \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d}. Якщо хочемо уникнути множення великих чисел, можна скоротити дроби, і навіть «навхрест».
Приклади множення дробів
- \frac{2}{3}\cdot\frac{1}{5} = \frac{2\cdot 1}{3\cdot 5}=\frac{2}{15}
- \frac{2}{3}\cdot\frac{3}{4} = \frac{2\cdot 3}{3\cdot 4}=\frac{2}{4}=\frac{1}{2} (зверніть увагу, що не множимо спочатку, а відразу скорочуємо)
Ділення дробів це те саме, що і множення на обернений дріб: \frac{a}{b}:\frac{c}{d} = \frac{a}{b}\cdot\frac{d}{c}=\frac{a\cdot d}{b\cdot c}.
Приклади ділення дробів
- \frac13:\frac12 =\frac13\cdot \frac21 = \frac23
- \frac{2}{5}:\frac{3}{4}=\frac{2}{5}\cdot \frac{4}{3} = \frac{2\cdot 4}{5\cdot 3} = \frac{8}{15}
