
Загальне рівняння прямої на площині

Загальне рівняння прямої на площині має вигляд: ax+by+c=0, де константи a та b є координатами нормалі, а c − дійсне число. Нормаль \vec{n}=(a;b) є вектором, перпендикулярним до даної прямої, а отже, і до вектора прямої.
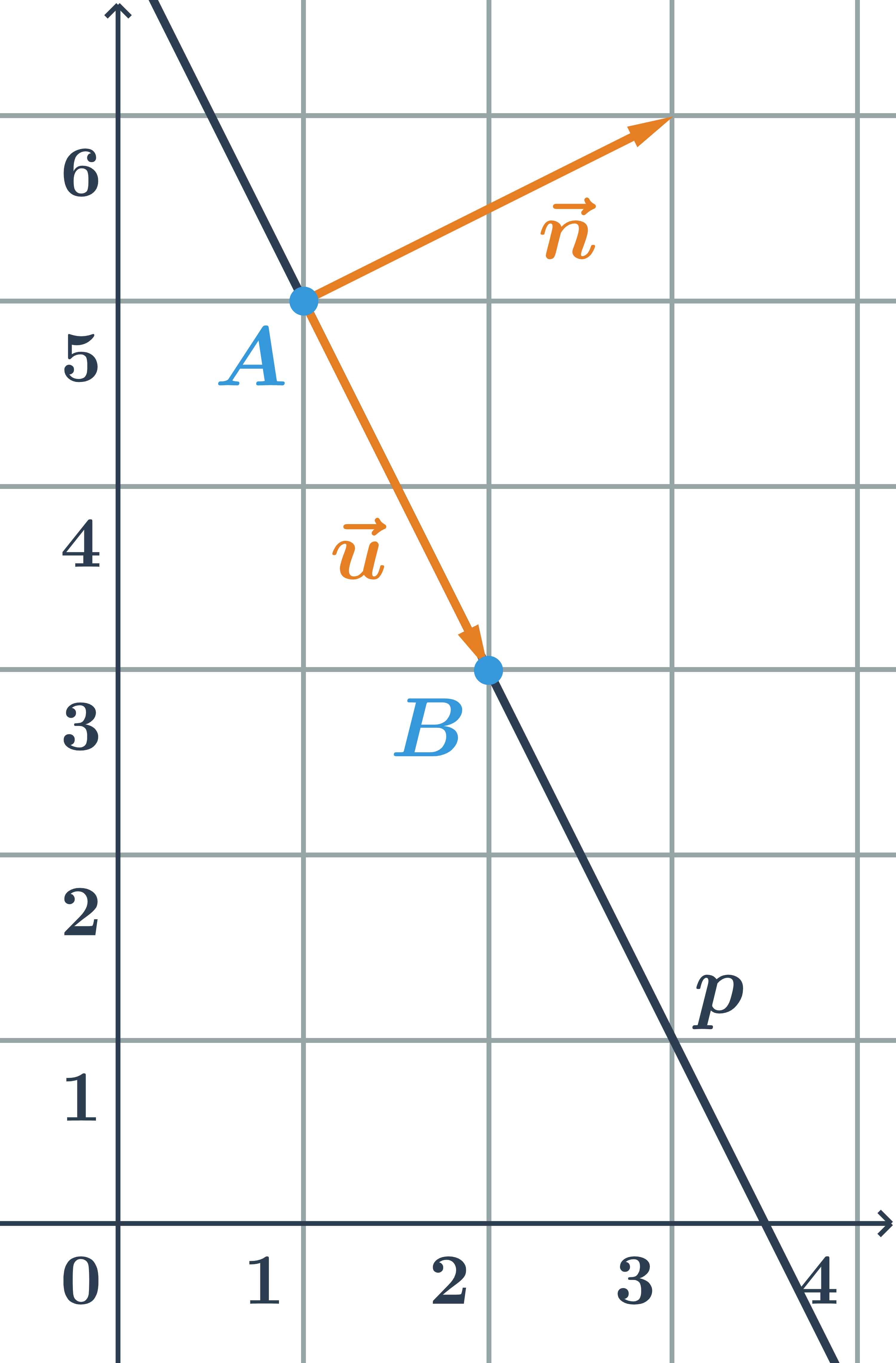
Загальне рівняння прямої p, заданої точками A=[1;5], a B=[2;3]
- Пряма p задана точкою A і вектором \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
- Нормаль є перпендикулярною до вектора \vec{u}=(1;-2), тобто наприклад, вектор \vec{n}=(2;1).
- Координати нормалі є константами a і b у загальному рівнянні прямої. Загальне рівняння має вигляд: 2x+y+c=0.
- Константу c знаходимо, підставивши координати точки A=[1;5] :
- 2\cdot1+5+c=0\Rightarrow c=-7.
- Загальне рівняння прямої p це: 2x+y-7=0.
Загальне рівняння прямої, заданої параметрично
Знайдіть загальне рівняння прямої p, яка задана такою параметричною системою рівнянь: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}
- Пряма p задана точкою A=[1;4] і вектором \vec{u}=(2;6).
- Координати вектора можна звести до вигляду: \vec{u}=(1;3).
- Нормаль є перпендикулярною до вектора \vec{u}=(1;3), тобто, наприклад, вектор \vec{n}=(3;-1).
- Координати нормалі є константами a та b у загальному рівнянні прямої. Загальне рівняння має вигляд: 3x-y+c=0.
- Константу c знаходимо, підставивши координати точки A=[1;4] :
- 3\cdot1-4+c=0\Rightarrow c=1.
- Загальне рівняння прямої p це: 3x-y+1=0.
Параметричне представлення прямої, заданої загальним рівнянням
Знайдіть параметричне представлення прямої p, яка має загальне рівняння: 3x-2y+4=0.
- Пряма p має нормаль \vec{n}=(3;-2).
- Вектор є перпендикулярним до вектора \vec{n}=(3;-2), тобто, наприклад, вектор \vec{u}=(2;3).
- Знайдемо одну точку на прямій p: одну координату можемо вибрати, наприклад, x=0, другу координату знайдемо: 3\cdot0-2y+4=0\Rightarrow y=2.
- Із загального рівняння ми визначили, що на прямій лежить точка A=[0;2].
- Параметричне представлення прямої p це: \begin{array}{rrl}x&=&0+2t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
Закрити










